Mean median slope – High School Geometry

Anyone who’s taken a stat course before may inadvertently misconstrue the title as “mean, median, mode” — and thereby get a slight shock, because we actually called “mean median slope”. After one recovers from this shock, one discovers that this post covers a leftover from our first post in this October. There, we went over some things hurriedly, which made this carryover necessary.

Excursion

As we hit the road, have your pencil, paper, and patience ready.

Find the slopes of the three medians of $\triangle ABC$ with vertices at $A(1,2)$ , $B(0,0)$ , $C(5,0)$ .

The midpoints of sides $AB$ , $BC$ , and $CA$ are $\left(\frac{1}{2},1\right)$ , $\left(\frac{5}{2},0\right)$ , and $(3,1)$ , respectively. Thus, the slopes of the medians are:

$m_A=-\frac{4}{3},~m_{B}=\frac{1}{3},~m_C=-\frac{2}{9}.$

What do you notice about the reciprocals $-\frac{9}{2},-\frac{3}{4},\frac{3}{1}$ ?

Find the slopes of the three medians of $\triangle ABC$ with vertices at $A(0,4)$ , $B(0,0)$ , $C(5,3)$ .

The midpoints of sides $AB,BC,CA$ are $(0,2)$ , $\left(\frac{5}{2},\frac{3}{2}\right)$ , $\left(\frac{5}{2},\frac{7}{2}\right)$ , respectively. Thus, the slopes of the medians are:

$m_A=-1,~m_B=\frac{7}{5},~m_C=\frac{1}{5}.$

Re-arrange them as $-1,\frac{1}{5},\frac{7}{5}$ . What do you notice?

PROVE that if a triangle has one side parallel to the $x$ -axis, then the reciprocals of the slopes of the three medians form an arithmetic progression.

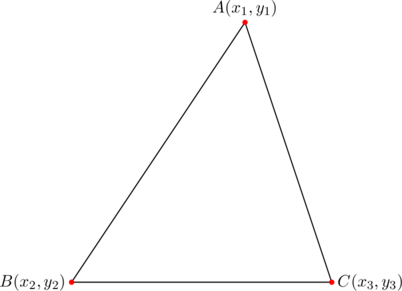
In the above diagram, let’s require that $y_2=y_3$ , so that side $BC$ is parallel to the $x$ -axis.

Normally, the slopes of the medians from vertices $A,B,C$ are:

$m_A=\frac{y_2+y_3-2y_1}{x_2+x_3-2x_1},~m_B=\frac{y_1+y_3-2y_2}{x_1+x_3-2x_2},~m_C=\frac{y_1+y_2-2y_3}{x_1+x_2-2x_3}.$

If we now put $y_2=y_3$ and consider the reciprocals

$\frac{1}{m_A}=\frac{x_2+x_3-2x_1}{2(y_2-y_1)},~\frac{1}{m_B}=\frac{x_1+x_3-2x_2}{y_1-y_2},~\frac{1}{m_C}=\frac{x_1+x_2-2x_3}{y_1-y_2}$

then

$\frac{1}{m_B}+\frac{1}{m_C}=\frac{2x_1-x_2-x_3}{y_1-y_2}=\frac{x_2+x_3-2x_1}{y_2-y_1}=2\times\frac{1}{m_A}.$

Thus, the reciprocals $\frac{1}{m_C},\frac{1}{m_A},\frac{1}{m_B}$ of the median slopes form an arithmetic progression, and the arithmetic mean of this progression is the slope of the median from the vertex opposite the side parallel to the $x$ -axis.

In the special case when $AB=AC$ , we have that the median from vertex $A$ is vertical, and so its slope is undefined. Nevertheless, since we’re concerned with the reciprocals of the slopes, the conclusion still holds. In fact, we obtain a special arithmetic progression $\frac{1}{m_C},0,\frac{1}{m_B}$ , where $m_B=-m_C$ .

Express the common difference of the arithmetic progression in the previous example in terms of the slopes of the parent triangle.

The arithmetic progression is $\frac{1}{m_C},\frac{1}{m_A},\frac{1}{m_B}$ . The common difference is the difference between consecutive terms; for example, $d=\frac{1}{m_B}-\frac{1}{m_A}$ :

(1) $\begin{equation*} \begin{split} \frac{1}{m_B}-\frac{1}{m_A}&=\left(\frac{x_1+x_3-2x_2}{y_1-y_2}\right)-\left(\frac{x_2+x_3-2x_1}{2(y_2-y_1)}\right)\\ &=\frac{2(x_1+x_3-2x_2)+(x_2+x_3-2x_1)}{2(y_1-y_2)}\\ &=\frac{3}{2}\left(\frac{x_3-x_2}{y_1-y_2}\right) \end{split} \end{equation*}$

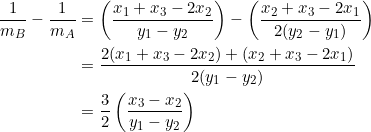
Consider the difference between the reciprocals of the slopes of sides $AB$ and $AC$ :

(2) $\begin{equation*} \begin{split} \frac{1}{m_{AB}}-\frac{1}{m_{AC}}&=\frac{x_1-x_2}{y_1-y_2}-\frac{x_1-x_3}{y_1-y_2}\\ &=\frac{x_3-x_2}{y_1-y_2} \end{split} \end{equation*}$

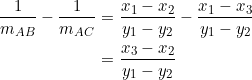
It follows from (1) and (2) that $d=\frac{3}{2}\left(\frac{1}{m_{AB}}-\frac{1}{m_{AC}}\right)$ .

converse results: click to read

The converse of example 3 and example 5 below will be shown in example 9 and example 8.

clockwise rotation: click to read

Having established the two preceding examples, the next two can be proved using rotations — specifically, a ninety degree (clockwise or counter-clockwise) rotation about a convenient center. Nevertheless, we’ll still use a direct method.

PROVE that if a triangle has one side parallel to the $y$ -axis, then the slopes of the three medians form an arithmetic progression.

Let the vertices be placed at $A(x_1,y_1)$ , $B(x_2,y_2)$ , $C(x_2,y_3)$ . Here, side $BC$ is parallel to the $y$ -axis. The slopes of the three medians are:

$m_A=\frac{y_2+y_3-2y_1}{2(x_2-x_1)},~m_B=\frac{y_1+y_3-2y_2}{x_1-x_2},~m_C=\frac{y_1+y_2-2y_3}{x_1-x_2}$

and so

$m_B+m_C=\frac{2y_1-y_2-y_3}{x_1-x_2}=2\times m_A\implies m_C,m_A,m_B~\textrm{form an AP}.$

Easy stuff.

Express the common difference of the arithmetic progression in the previous example in terms of the slopes of the parent triangle.

Let the common difference be $d$ . Using the median slopes in the preceding example, we have:

$\begin{equation*} \begin{split} d&=m_B-m_A\\ &=\left(\frac{2(y_1+y_3-2y_2)}{2(x_1-x_2)}\right)-\left(\frac{y_2+y_3-2y_1}{2(x_2-x_1)}\right)\\ &=\frac{3}{2}\left(\frac{y_3-y_2}{x_1-x_2}\right) \end{split} \end{equation*}$

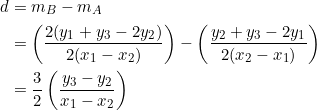
Consider the difference between the slopes of sides $CA$ and $AB$ :

$m_{CA}-m_{AB}=\frac{y_3-y_1}{x_2-x_1}-\frac{y_2-y_1}{x_2-x_1}=\frac{y_3-y_2}{x_2-x_1}.$

Thus, $d=\frac{3}{2}(m_{AB}-m_{CA})$ .

Exception

In fact, exceptional. In the case of a right triangle with legs parallel to the coordinate axes, something interesting happens.

PROVE that if a right triangle has legs parallel to the coordinate axes, then the slopes of the three medians form a geometric progression with $r=-2$ , and when re-arranged, form an arithmetic progression.

Suppose the situation is pictured below:

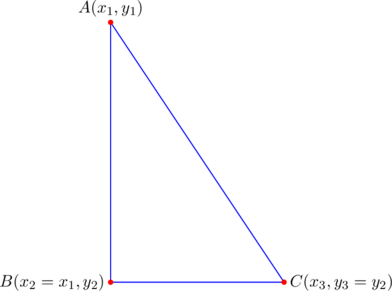
and let’s apply, as an informal argument, an exercise from our immediate past post. That exercise says that if $a,b,c$ form an arithmetic progression and at the same time the reciprocals $\frac{1}{a},\frac{1}{b},\frac{1}{c}$ form another arithmetic progression (in the same order), then the relation $b^2=ac$ holds — which is a condition for $a,b,c$ to be a geometric progression.

In the present case, because side $BC$ is parallel to the $x$ -axis, we have (by example 3) that the reciprocals $\frac{1}{m_C},\frac{1}{m_A},\frac{1}{m_B}$ of the median slopes form an arithmetic progression. Similarly, since side $AB$ is parallel to the $y$ -axis, we have (by example 5) that the median slopes $m_C,m_A,m_B$ form an arithmetic progression. Together, we arrive at a scenario described in the previous paragraph. This sheds a little light on why the median slopes behave specially in this case.

We can continue this informal argument to show that the common ratio of the geometric progression is $r=-2$ , but there’s a simpler, more direct alternative:

$m_C=\frac{y_1-y_2}{2(x_1-x_2)},~m_B=-\left(\frac{y_1-y_2}{x_1-x_2}\right),~m_A=2\left(\frac{y_1-y_2}{x_1-x_2}\right).$

The geometric progression is $m_C,m_B,m_A$ and the common ratio is $r=-2$ . At the same time, we have an arithmetic progression $m_A,m_C,m_B$ because $m_A+m_B=2\times m_C$ .

Extensions

Suppose that the slopes of the medians of $\triangle ABC$ form an arithmetic progression $m_C,m_A,m_B$ with common difference $d=\frac{3}{2}\left(m_{AB}-m_{AC}\right)$ . PROVE that side $BC$ is parallel to the $y$ -axis.

As you’ll notice, this is the converse of example 5. The proof is simple, but involves some algebraic manipulations. So we present a snapshot below.

Let the vertices be $A(x_1,y_1)$ , $B(x_2,y_2)$ , $C(x_3,y_3)$ . Since $m_A-m_C=d$ , we have:

(3) $\begin{equation*} \frac{y_2+y_3-2y_1}{x_2+x_3-2x_2}-\frac{y_1+y_2-2y_3}{x_1+x_2-2x_3}=\frac{3}{2}\left(\frac{y_1-y_2}{x_1-x_2}-\frac{y_1-y_3}{x_1-x_3}\right) \end{equation*}$

After some simplifications, this reduces to:

$\left[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\right]\left[(x_2-x_3)(x_2+2x_3-3x_1)\right]=0.$

The expression in the first square bracket, namely

$x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2),$

cannot be zero (it actually represents twice the triangle area). This forces

(4) $\begin{equation*} (x_2-x_3)(x_2+2x_3-3x_1)=0 \end{equation*}$

Also, $m_B-m_A=d$ implies

(5) $\begin{equation*} \frac{y_1+y_3-2y_2}{x_1+x_3-2x_2}-\frac{y_2+y_3-2y_1}{x_2+x_3-2x_1}=\frac{3}{2}\left(\frac{y_1-y_2}{x_1-x_2}-\frac{y_1-y_3}{x_1-x_3}\right) \end{equation*}$

Simplifying, we obtain

$\left[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\right]\left[(x_2-x_3)(3x_1-2x_2-x_3)\right]=0$

and we are forced to take

(6) $\begin{equation*} (x_2-x_3)(3x_1-2x_2-x_3)=0 \end{equation*}$

Let’s combine (4) and (6):

$(x_2-x_3)\left[x_2+2x_3-3x_1) + (3x_1-2x_2-x_3)\right]=0.$

Thus, $(x_2-x_3)(x_3-x_2)=0\implies x_2=x_3$ , showing that side $BC$ is parallel to the $y$ -axis.

Suppose that the reciprocals of the slopes of the medians of $\triangle ABC$ form an arithmetic progression $\frac{1}{m_C},\frac{1}{m_A},\frac{1}{m_B}$ with common difference $d=\frac{3}{2}\left(\frac{1}{m_{AB}}-\frac{1}{m_{AC}}\right)$ . PROVE that side $BC$ is parallel to the $x$ -axis.

Because the proof is similar to the previous one, we omit it. Just take our word for its validity; better still, try it as an activity.

Consider two right triangles in which the legs have the same slopes, but the hypotenuse of one is parallel to the $x$ -axis, while the hypotenuse of the other is parallel to the $y$ -axis. PROVE that in both cases, the common differences of the arithmetic progressions formed by the slopes of the medians are equal.

One may think that this has something to do with similarity, but it’s more than that.

The reason it happens is simple. In example 4, the common difference of the reciprocals of the median slopes when one side is parallel to the $x$ -axis was given by

$d_1=\frac{3}{2}\left(\frac{1}{m_{AB}}-\frac{1}{m_{AC}}\right).$

In In example 6, the common difference of the median slopes when one side is parallel to the $y$ -axis was

$d_2=\frac{3}{2}\left(m_{AB}-m_{AC}\right).$

If these two common differences should be equal, then

$\frac{1}{m_{AB}}-\frac{1}{m_{AC}}=\left(m_{AB}-m_{AC}\right)\implies m_{AB}\times m_{AC}+1=0.$

So the triangle must be a right triangle. Similarity is not enough. To see this, consider $\triangle ABC$ with vertices at $A(4,6)$ , $B(0,0)$ , $C(14,0)$ . The reciprocals of the slopes of the three medians are:

$-4,-\frac{1}{2},3\implies d_1=\frac{7}{2}.$

Now consider $\triangle A'B'C'$ with vertices at $A'\left(\frac{20}{3},10\right)$ , $B'(0,0)$ , $C'(0,14)$ . Notice that $\triangle A'B'C'$ is similar to $\triangle ABC$ . However, the slopes of the three medians of $\triangle A'B'C'$ are

$-\frac{27}{10},~\frac{9}{20},~\frac{36}{10}\implies d_2=\frac{16}{5}\neq \frac{7}{2}=d_1.$

Takeaway

For any $\triangle ABC$ , the following two conditions are equivalent:

side $BC$ is parallel to the $x$ -axis;
the reciprocals of the median slopes form an arithmetic progression $\frac{1}{m_C}$ , $\frac{1}{m_A}$ , $\frac{1}{m_B}$ with common difference $d=\frac{3}{2}\left(\frac{1}{m_{AB}}-\frac{1}{m_{AC}}\right)$ .

Similarly, the following two conditions are equivalent for any $\triangle ABC$ :

side $BC$ is parallel to the $y$ -axis;
the median slopes form an arithmetic progression $m_C$ , $m_A$ , $m_B$ with common difference $d=\frac{3}{2}\left(m_{AB}-m_{AC}\right)$ .

Beautiful, simple things.

Tasks

(Isosixless triangle) Let be isosceles such that .
- if the base $BC$ is parallel to the $x$ -axis, PROVE that $\frac{m_{BC}}{m_A}+\frac{m_{CA}}{m_B}+\frac{m_{AB}}{m_C}=-6$ ;
- if the base $BC$ is parallel to the $y$ -axis, PROVE that $\frac{m_{A}}{m_{BC}}+\frac{m_{B}}{m_{CA}}+\frac{m_{C}}{m_{AB}}=-6$ .
  (Beautiful scenes. More in exercise 2 below.)
(Isosixless triangle) Consider with vertices at , , , where . (Side is parallel to the -axis.)
- PROVE that $\frac{m_{BC}}{m_A}+\frac{m_{CA}}{m_B}+\frac{m_{AB}}{m_C}=\frac{2(x_1^2+x_2^2+x_3^2-x_1x_2-x_2x_3-x_3x_1)}{(x_1-x_2)(x_1-x_3)}$ .
- Deduce that $\frac{m_{BC}}{m_A}+\frac{m_{CA}}{m_B}+\frac{m_{AB}}{m_C}=-6$ if, and only if, $2x_1=x_2+x_3$ .
  (Among all triangles with one side parallel to the $x$ -axis, only the isosceles triangle has the property that $\frac{m_{BC}}{m_A}+\frac{m_{CA}}{m_B}+\frac{m_{AB}}{m_C}=-6$ . Hence the name isosixless.)
(Equilateral triangle) Let be equilateral with side-slopes , , and median-slopes , , .
- PROVE that $\frac{m_{BC}}{m_A}+\frac{m_{CA}}{m_B}+\frac{m_{AB}}{m_C}=-\left(m_{BC}^2+m_{CA}^2+m_{AB}^2\right)$ .
- Using the above and exercise 1, deduce that if side $BC$ is parallel to the $x$ -axis, then the slopes of the other two sides are $\pm\sqrt{3}$ .
- PROVE that the side-slopes form an arithmetic progression if, and only if, $\frac{m_{BC}}{m_A}+\frac{m_{CA}}{m_B}+\frac{m_{AB}}{m_C}=-6.$
- PROVE that the side-slopes form a geometric progression if, and only if, $\frac{m_{BC}}{m_A}+\frac{m_{CA}}{m_B}+\frac{m_{AB}}{m_C}=-15.$
  (Beautiful scenes.)
Verify that the solutions to the polynomial equation $9m^6-135m^4+135m^2-9=0$ are $\pm 1$ , $2\pm\sqrt{3}$ , $-2\pm\sqrt{3}$ .
(Reversible sequence) PROVE that any three-term geometric progression with common ratio $r=-2$ can always be re-arranged to form a three-term arithmetic progression.
Let $a,b,c$ be distinct numbers and suppose that $c,a,b$ form an arithmetic sequence while $a,c,b$ form a geometric sequence. PROVE that the common ratio of the geometric sequence is necessarily $r=-2$ . (Compare with the preceding exercise.)
Let , , and denote the slopes of medians from vertices , , and . Find a triangle for which the following three relations hold simultaneously:
- $\frac{1}{m_B}+\frac{1}{m_C}=\frac{2}{m_A}$ ;
- $m_A\times m_B=2\times m_C$ ;
- $m_A=2(m_B-1)$ . (Implied by the first two.)
If the “base” of an isosceles triangle is parallel to the -axis, PROVE that the slopes of the two equal sides are opposites of each other. Thus, the side-slopes will form an arithmetic progression of the form . Furthermore, PROVE that:
- $m_B=\frac{1}{3}m_{AB}$
- $m_C=-\frac{1}{3}m_{CA}$ .
  (If the “base” of an isosceles triangle is parallel to the $y$ -axis, the slopes of the three medians form an arithmetic progression of the form $-k,0,k$ .)
Consider with vertices at , , , where is fixed.
- Verify that the median slopes are $m_A=\frac{\alpha-4}{12}$ , $m_B=\frac{\alpha+8}{12}$ , $m_C=\frac{\alpha-16}{12}$ , and that they form an arithmetic progression $m_C,m_A,m_B$ with common difference $d=1$ .
  (It’s somewhat interesting that this common difference stays the same as $\alpha$ varies.)
- Find the value of $\alpha$ for which the arithmetic sequence above becomes a geometric sequence with common ratio $r=-2$ .
Find coordinates for the vertices of in which:
- the slopes of the three medians are $-3,-2,-1$ .
- the slopes of the three medians are $1,2,3$ .
- the slopes of the three medians are $-2,-1,0$ .
- the slopes of the three medians are $-1,0,1$ .
- the slopes of the three medians are $0,1,2$ .