Doubtless, it’s quite careless — if not senseless — to name a triangle isosixless. Unless an attempt is made to buttress the use of such an address, one’ll never be impressed by the meaningless, lame name.
Given any triangle ![]() , take the quotient of the slope of each median and the slope of the opposite side, and form the sum
, take the quotient of the slope of each median and the slope of the opposite side, and form the sum
(1) ![]()
Among all triangles with one side parallel to the ![]() -axis (or
-axis (or ![]() -axis), it’s only the isosceles triangle that satisfies
-axis), it’s only the isosceles triangle that satisfies ![]() . Thus, we thought it might be apt to adapt isosceles as isosixless, in view of
. Thus, we thought it might be apt to adapt isosceles as isosixless, in view of ![]() . Now, beat that.
. Now, beat that.
For ![]() with vertices at
with vertices at ![]() ,
, ![]() ,
, ![]() , verify that
, verify that ![]() , where
, where ![]() is given by equation (1).
is given by equation (1).
A quick calculation shows that
![]()
and so
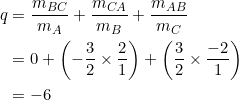
No doubt about that.
Negative partsixtions
Normally, partitions are not defined for negative integers, but with your permission, we’re doing so for this discussion. Taking two/three numbers at a time, we can write
![]()
We’ll show that only the “partition” ![]() works, and yields a characterization of isosceles triangles.
works, and yields a characterization of isosceles triangles.
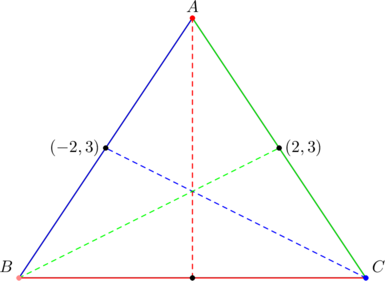
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() ,
, ![]() . PROVE that
. PROVE that
![]()
where ![]() represents the sum of quotients
represents the sum of quotients ![]() .
.
We have:
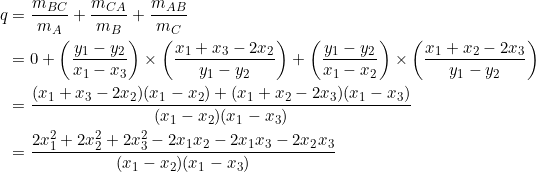
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() ,
, ![]() . PROVE that
. PROVE that
![]()
if and only if ![]() .
.
First suppose that ![]() . After clearing fractions and combining like terms, we obtain
. After clearing fractions and combining like terms, we obtain
![]()
where the left side is precisely the expansion of ![]() . Thus,
. Thus, ![]() .
.
Conversely, suppose that ![]() . Then:
. Then:
In any ![]() , PROVE that
, PROVE that ![]() and
and ![]() if and only if
if and only if ![]() is isosceles with side
is isosceles with side ![]() parallel to the
parallel to the ![]() -axis.
-axis.
Thus, ![]() only when two of the summands in (1) are both
only when two of the summands in (1) are both ![]() .
.
We show one direction of the proof — that both ![]() and
and ![]() yield an isosceles triangle with one side parallel to the
yield an isosceles triangle with one side parallel to the ![]() -axis.
-axis.
Place the vertices of ![]() at
at ![]() ,
, ![]() ,
, ![]() . The first condition
. The first condition ![]() amounts to
amounts to
![]()
Clear fractions and combine similar terms:
(2) ![]()
The second condition ![]() , in terms of the given coordinates, is:
, in terms of the given coordinates, is:
![]()
Clear fractions and combine like terms:
(3) ![]()
Subtract equation (2) from equation (3):
![]()
This factors as ![]() . We claim that both
. We claim that both ![]() and
and ![]() must hold. If not, suppose that only
must hold. If not, suppose that only ![]() holds and re-calculate the quotient
holds and re-calculate the quotient ![]() :
:
![]()
This doesn’t equal ![]() unless we impose
unless we impose ![]() . Thus, we must have
. Thus, we must have ![]() (side
(side ![]() parallel to the
parallel to the ![]() -axis) and
-axis) and ![]() (which, in conjunction with
(which, in conjunction with ![]() yields an isosceles triangle).
yields an isosceles triangle).
For an equilateral triangle ![]() , PROVE that
, PROVE that
![]()
This is a consequence of the fact that the medians in an equilateral triangle are perpendicular to the opposite sides. In particular:
![]()
ignoring any zero denominator. Then:
![]()
The above example can be used to explain why the side-slopes of an equilateral triangle with side ![]() parallel to the
parallel to the ![]() -axis are
-axis are ![]() and
and ![]() .
.
Native progressions
![]()
where ![]() is the slope of one of the sides. The fact that the slopes can be expressed in terms of the slope of one side leads to some interesting consequences.
is the slope of one of the sides. The fact that the slopes can be expressed in terms of the slope of one side leads to some interesting consequences.
PROVE that the slopes of the sides of an equilateral triangle form an arithmetic progression if, and only if, one of the slopes is zero.
First suppose that one of the slopes is zero. There are three possibilities:
 . That is,
. That is,  (since
(since  as per above). In this case we have:
as per above). In this case we have:
![Rendered by QuickLaTeX.com \[m_2=\frac{m-\sqrt{3}}{1+\sqrt{3}m}=-\sqrt{3},~m_3=\frac{m+\sqrt{3}}{1-\sqrt{3}m}=\sqrt{3},\]](//blog.fridaymath.com/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
and so we obtain the arithmetic progression
 corresponding to
corresponding to  .
. . This implies
. This implies  , and so
, and so  . In other words,
. In other words,  . This also gives
. This also gives
![Rendered by QuickLaTeX.com \[m_3=\frac{m+\sqrt{3}}{1-\sqrt{3}m}=\frac{\sqrt{3}+\sqrt{3}}{1-\sqrt{3}\times\sqrt{3}}=-\sqrt{3}.\]](//blog.fridaymath.com/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
We obtain an arithmetic progression
 this time around.
this time around. . This implies
. This implies  , and so
, and so  . That is,
. That is,  . With this
. With this
![Rendered by QuickLaTeX.com \[m_2=\frac{m-\sqrt{3}}{1+\sqrt{3}m}=\frac{-\sqrt{3}-\sqrt{3}}{1+\sqrt{3}\times(-\sqrt{3})}=\sqrt{3},\]](//blog.fridaymath.com/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
giving the arithmetic progression

For the converse, suppose that the side-slopes form an arithmetic progression. There are three cases to consider: the progression could be ![]() , or
, or ![]() or
or ![]() .
.
PROVE that the slopes of the sides of an equilateral triangle form an arithmetic progression if, and only if, ![]() .
.
If the slopes form an arithmetic progression, then one of them must be zero, in view of example 6. Since an equilateral triangle is also isosceles, we have (by example 3) that ![]() .
.
On the other hand, suppose that ![]() . Using example 5 and the expressions for the slopes of the sides of an equilateral triangle, we have:
. Using example 5 and the expressions for the slopes of the sides of an equilateral triangle, we have:
![Rendered by QuickLaTeX.com \[m^2+\left(\frac{m-\sqrt{3}}{1+\sqrt{3}m}\right)^2+\left(\frac{m+\sqrt{3}}{1-\sqrt{3}m}\right)^2=6.\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-45889440a94444a5fd778aa5331dd0ed_l3.png)
Afer simplifications, this leads to
![]()
Taking each of these three values of ![]() in turn, we see that the side-slopes form an arithmetic progression (similar to example 6).
in turn, we see that the side-slopes form an arithmetic progression (similar to example 6).
Solve the sixth-degree polynomial equation ![]() .
.
By the way, such an equation is also sometimes called “bicubic” (just like “biquadratic”), since the odd degree terms are missing.
The form of the coefficients in this polynomial equation means that we can re-arrange the terms and factor systematically:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} 9m^6-135m^4+135m^2-9&=0\\ (9m^6-9)+(-135m^4+135m^2)&=0\\ 9(m^6-1)-135m^2(m^2-1)&=0\\ 9[(m^2)^3-1]-135m^2(m^2-1)&=0\\ 9(m^2-1)(m^4+m^2+1)-135m^2(m^2-1)&=0\\ 9(m^2-1)(m^4+m^2+1-15m^2)&=0\\ (m^2-1)(m^4-14m^2+1)&=0 \end{split} \end{equation*}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-68fb699285f05fd08273a0c05cfdee68_l3.png)
The first quadratic factor, ![]() , has
, has ![]() as solutions. The second “biquadratic” factor,
as solutions. The second “biquadratic” factor, ![]() , has solutions that can be obtained from the quadratic formula:
, has solutions that can be obtained from the quadratic formula:
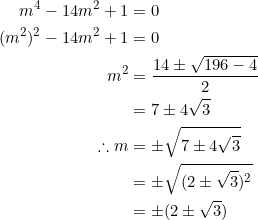
Thus, we obtain six solutions
![]()
PROVE that the slopes of the sides of an equilateral triangle form a geometric progression if, and only if, one of the slopes is ![]() .
.
This is the geometric progression version of example 6. First suppose that the slopes form a geometric progression. There are three cases to consider:
-
 is the geometric mean of the progression. In this case we have:
is the geometric mean of the progression. In this case we have: -
 is the geometric mean of the progression. In this case we have:
is the geometric mean of the progression. In this case we have: -
 is the geometric mean of the progression. In this case we have:
is the geometric mean of the progression. In this case we have:
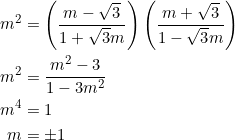
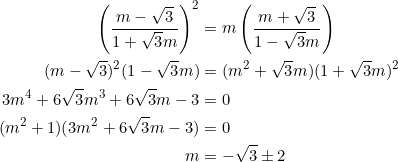
If ![]() , then
, then ![]() becomes
becomes ![]() , and if
, and if ![]() , then
, then ![]() is
is ![]() . So we get that one of the slopes is
. So we get that one of the slopes is ![]() .
.
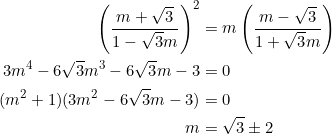
If ![]() , then
, then ![]() is
is ![]() , and if
, and if ![]() , then
, then ![]() evaluates to
evaluates to ![]() .
.
Conversely, if one of the slopes is ![]() , it is also easy to see that the other slopes combine to form a geometric progression.
, it is also easy to see that the other slopes combine to form a geometric progression.
PROVE that the slopes of the sides of an equilateral triangle form a geometric progression if, and only if, ![]() .
.
First suppose that ![]() . Using the expression for
. Using the expression for ![]() in example 5 and the expressions for the side-slopes of an equilateral triangle, we have:
in example 5 and the expressions for the side-slopes of an equilateral triangle, we have:
![Rendered by QuickLaTeX.com \[m^2+\left(\frac{m-\sqrt{3}}{1+\sqrt{3}m}\right)^2+\left(\frac{m+\sqrt{3}}{1-\sqrt{3}m}\right)^2=15,\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-b719a6abed96d4aaae806b93f0d393e6_l3.png)
which, after simplifications, leads to the sixth-degree equation
![]()
same as the one in example 8. Since the solutions are ![]() ,
, ![]() ,
, ![]() , the side-slopes form a geometric progression.
, the side-slopes form a geometric progression.
Conversely, if the side-slopes form a geometric progression, all possiblities can be enumerated. For example, we can have ![]() ,
, ![]() ,
, ![]() . Using example 5 again we have:
. Using example 5 again we have:
![]()
That is, ![]() . Other combinations of
. Other combinations of ![]() also yield
also yield ![]() .
.
In a future post we may form the sum:
(4) ![]()
If an equilateral triangle does not have any of its sides parallel to the coordinate axes, then ![]() . Accordingly, any triangle that satisfies (4) will be called equilessthree, a name as lame as isosixless.
. Accordingly, any triangle that satisfies (4) will be called equilessthree, a name as lame as isosixless.
Takeaway
For an equilateral ![]() , the following statements are equivalent:
, the following statements are equivalent:
- one of the side-slopes is zero;
- the sum of the side-slopes is zero;
- the side-slopes form an arithmetic progression;
 , where
, where  is the sum of quotients
is the sum of quotients  .
.
Similarly, the following conditions are equivalent for an equilateral ![]() :
:
- one of the side-slopes is plus/minus one;
- the sum of the side-slopes is plus/minus three;
- the side-slopes form a geometric progression;
 , where
, where  is the sum of quotients
is the sum of quotients  .
.
So much about slopes in our posts, eh? Probably a reason we tend to be sloppy with words and stuff?
Tasks
- (Minus one) Let
 . If, in
. If, in  we have the relations
we have the relations  ,
,  ,
,  :
:
- PROVE that
 .
. - Discuss what happens when
 . Interesting case.
. Interesting case.
- PROVE that
- Let
 and
and  be real numbers.
be real numbers.
- PROVE that the quadratic equation
 has no real solutions.
has no real solutions. - Deduce that
 if, and only if,
if, and only if,  .
.
- PROVE that the quadratic equation
- PROVE that
 in an equilateral triangle
in an equilateral triangle  with non-zero side-slopes.
with non-zero side-slopes. - In
 , let the slopes of sides
, let the slopes of sides  be
be  , respectively. PROVE that
, respectively. PROVE that  .
. - PROVE that the relations
 ,
,  ,
,  are not possible simultaneously.
are not possible simultaneously. - Solve the quartic equation
 .
. - In
 , let the slopes of sides
, let the slopes of sides  be in geometric progression
be in geometric progression  . PROVE that
. PROVE that  .
.
(Things always become interesting in the setting of geometric progressions. Always.) - In
 , let the slopes of sides
, let the slopes of sides  be in geometric progression
be in geometric progression  . PROVE that
. PROVE that  .
.
(Things always become interesting in the setting of geometric progressions. Always.) - (Simplified area) In
 , let
, let  be the slopes of sides
be the slopes of sides  , where
, where  ,
,  ,
,  are the coordinates of the vertices. PROVE that the area of
are the coordinates of the vertices. PROVE that the area of  can be given by
can be given by  .
.
(Absolute value may be needed in the final result.) - PROVE that there is no triangle
 for which the relations
for which the relations  ,
,  , and
, and  hold simultaneously.
hold simultaneously.
(You can use exercise 1 above.)