It’s becoming our tradition to have special editions on Thanksgiving occasions, and this year is no exception. Thus, there’s a brief digression from our familiar and friendly and favourite geometric progression, to arithmetic progression.
Golden ratio
The main equation for today’s consideration is
(1) ![]()
There’ll be explanation for it in examples 9 and 10. For now, look what we get if we set ![]() :
:
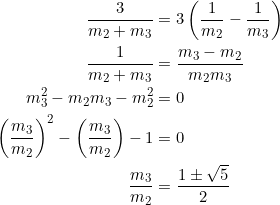
a.k.a golden ratio. You’ve seen this before here, and you’ll meet it again before the end of this year.
Gentle reminder
Kindly remember that the due date to hand in your solutions to examples 1 through 8 is October 28. Please don’t hesitate, don’t leave it late.
It is located at ![]() .
.
It is located at ![]() .
.
It is the point ![]() , and it lies on the circumcircle of
, and it lies on the circumcircle of ![]() .
.
We use examples 1 and 3. Specifically, the midpoint of ![]() and
and ![]() is precisely the circumcenter
is precisely the circumcenter ![]() .
.
Since ![]() is on the circumcircle and the midpoint of
is on the circumcircle and the midpoint of ![]() and
and ![]() is the center of this circle, it follows that
is the center of this circle, it follows that ![]() is also on the circumcircle.
is also on the circumcircle.
Use example 4 above.
Side ![]() is parallel to the
is parallel to the ![]() -axis this time around. The orthocenter is located at
-axis this time around. The orthocenter is located at ![]() .
.
It is the point ![]() .
.
It is the point ![]() .
.
Geometric result
(First “Theorem”)
In ![]() , let
, let ![]() and
and ![]() be the slopes of sides
be the slopes of sides ![]() and
and ![]() , with side
, with side ![]() parallel to the
parallel to the ![]() -axis. Let
-axis. Let ![]() be the orthocenter and let
be the orthocenter and let ![]() be the reflection of the orthocenter along side
be the reflection of the orthocenter along side ![]() . Then there is a point
. Then there is a point ![]() on the circumcircle of
on the circumcircle of ![]() such that the slopes of the medians of
such that the slopes of the medians of ![]() form an arithmetic progression with common difference
form an arithmetic progression with common difference ![]() , where
, where ![]() .
.
As you traverse the sides ![]() of
of ![]() you get familiar terms: Human Resources, Registered Nurse, Northern Hemisphere. You’ll never forget
you get familiar terms: Human Resources, Registered Nurse, Northern Hemisphere. You’ll never forget ![]() .
.
For convenience, place the vertices of ![]() at the points
at the points ![]() ,
, ![]() ,
, ![]() . Let
. Let ![]() be as given in examples 2,3,4:
be as given in examples 2,3,4:
![]()
The midpoints of sides ![]() are:
are:
![]()
respectively. And so the slopes of the medians from ![]() are:
are:
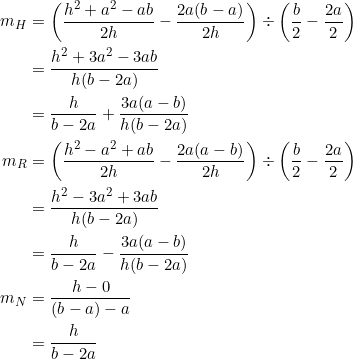
We get an arithmetic progression ![]() with common difference
with common difference
![]()
Returning to the parent triangle ![]() , we have
, we have
![]()
Then, then, and then
![]()
(Second “Theorem”)
In ![]() , let
, let ![]() be the slopes of sides
be the slopes of sides ![]() , with side
, with side ![]() parallel to the
parallel to the ![]() -axis. Let
-axis. Let ![]() be the orthocenter and let
be the orthocenter and let ![]() be the reflection of the orthocenter along side
be the reflection of the orthocenter along side ![]() . Then there is a point
. Then there is a point ![]() on the circumcircle of
on the circumcircle of ![]() such that the reciprocals of the slopes of the medians of
such that the reciprocals of the slopes of the medians of ![]() form an arithmetic progression with common difference
form an arithmetic progression with common difference ![]() , where
, where ![]() .
.
For convenience, place the vertices at ![]() ,
, ![]() ,
, ![]() . Take the orthocenter
. Take the orthocenter ![]() , its reflection
, its reflection ![]() along side
along side ![]() , and the point
, and the point ![]() . The mipoints of sides
. The mipoints of sides ![]() are:
are:
![]()
respectively. The slopes of the medians are then
![]()
and their reciprocals (re-arranged) are
![]()
These form an arithmetic sequence with common difference ![]() , where
, where
![]()
In terms of the parent triangle ![]() (vertices at
(vertices at ![]() ,
, ![]() ,
, ![]() ), we get:
), we get:
![]()
Takeaway
The construction we’ve done is true more generally, as follows:
- If a triangle has one side parallel to the
 -axis, then the reciprocals of the slopes of the three medians form an arithmetic progression;
-axis, then the reciprocals of the slopes of the three medians form an arithmetic progression; - If a triangle has one side parallel to the
 -axis, then the slopes of the three medians form an arithmetic progression.
-axis, then the slopes of the three medians form an arithmetic progression.
Tasks
- Suppose that the enumeration
 represents an arithmetic progression of distinct, non-zero numbers.
represents an arithmetic progression of distinct, non-zero numbers.
- if
 is also arithmetic, PROVE that
is also arithmetic, PROVE that  .
. - if
 is also arithmetic, PROVE that
is also arithmetic, PROVE that  .
. - if
 is also arithmetic, PROVE that
is also arithmetic, PROVE that  .
.
- if
- Find three distinct, non-zero numbers
 in arithmetic progression for which the reciprocals
in arithmetic progression for which the reciprocals  are also in arithmetic progression.
are also in arithmetic progression. - Find three distinct, non-zero numbers
 in arithmetic progression for which the reciprocals
in arithmetic progression for which the reciprocals  are also in arithmetic progression.
are also in arithmetic progression. - (Registered Nurse) For
 with vertices at
with vertices at  ,
,  , and
, and  , PROVE that the points
, PROVE that the points  and
and  are end points of a diameter of the circumcircle of
are end points of a diameter of the circumcircle of  .
. - Find coordinates for the vertices of a triangle in which the slopes of the three medians are
 .
.
Nationally, Thanksgiving is just one day — this past Monday; naturally, ours lasts more days, many days — being our mainstay. Our style of incorporating Thanksgiving into an “academic setting” is not very popular, and you may not be familiar with it. It’s part of what makes us peculiar; and in particular, it’s due to a spectacular event on Thursday, June 14, 2018: beautiful, remarkable, unforgettable day. Consequently (and continuously and conspicuously), the poster expresses gratitude to the Ancient of Days. All things being equal, our next iteration of Thanksgiving comes up on Monday, June 14, 2021. Until then, please understand that this practice is very useful for us, as we’re hopeful that we’ll always be mindful of the need to be grateful.
Thanksgiving