Euler points as reflected midpoints

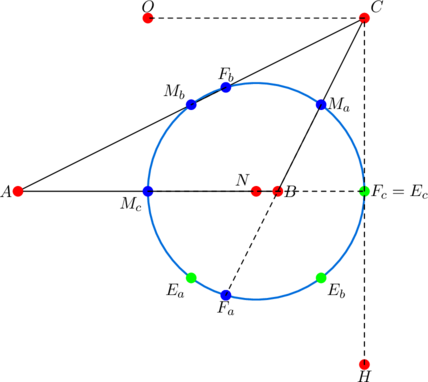
Of the nine main points through which the nine-point circle passes, three of them are Euler points: the midpoints of the line segments joining the orthocenter to each vertex (for example, the three green dots $E_a,E_b,E_c$ in the diagram below).

Owing to the equation

(1) $\begin{equation*} (b^2-a^2)^2=(ac)^2+(cb)^2 \end{equation*}$

only eight (rather than nine) points are present in the above nine-point circle, as the Euler point $E_c$ is forced to coincide with the foot of the altitude from vertex $C$ . At the same time, the two Euler points $E_a$ and $E_b$ correspond to the reflections of the midpoints of sides $AC$ and $BC$ over side $AB$ .

In $\triangle ABC$

, let $E_a$

be the Euler point associated with vertex $A$

. PROVE that equation (1) implies (and is implied by) $AE_a=\frac{b}{2}$

First suppose that $AE_a=\frac{b}{2}$ and let $R$ be the radius of the circumcircle of triangle $ABC$ .

By definition of the Euler points, $E_a$ is the midpoint of the segment joining vertex $A$ to the orthocenter $H$ . Since $AH=\sqrt{4R^2-a^2}$ in any triangle, we have that $AE_a=\frac{\sqrt{4R^2-a^2}}{2}$ . By the assumption we then have:

$\frac{\sqrt{4R^2-a^2}}{2}=\frac{b}{2}\implies a^2+b^2=4R^2$

By one of the equivalent statements here, we conclude that equation (1) holds. The converse is similar.

In $\triangle ABC$

, let $E_b$

be the Euler point associated with vertex $B$

. PROVE that equation (1) implies (and is implied by) $AE_b=\frac{a}{2}$

Just as in example 1 above.

If the side-lengths of $\triangle ABC$

satisfy equation (1), PROVE that $M_b$

is the reflection of $E_a$

over side $AB$

Consider $\triangle AE_aM_b$ . Since $AE_a=\frac{b}{2}$ from example 1 and $AM_b=\frac{b}{2}$ by definition, we have that $\triangle AE_aM_b$ is isosceles with base $E_aM_b$ . The altitude through $A$ bisects the base and so $E_a$ is a reflection of $M_b$ over side $AB$ .

If the side-lengths of $\triangle ABC$

satisfy equation (1), PROVE that $M_a$

is the reflection of $E_b$

over side $AB$

Consider $\triangle AE_bM_a$ and use example 2.

In $\triangle ABC$

, let $E_b$

be the Euler point associated with vertex $B$

. PROVE that equation (1) implies (and is implied by) $BE_b=\frac{a}{2}$

Just as in example 1.

Takeaway

In triangle $ABC$ , let $E_a, E_b,E_c$ denote the Euler points, $F_c$ the foot of the altitude from vertex $C$ , and $M_a,M_b,M_c$ the midpoints of sides $BC,CA,AB$ . Then the following statements are equivalent:

$E_c=F_c$
$AE_a=\frac{b}{2}$
$BE_b=\frac{a}{2}$
$E_a$ is the reflection of $M_b$ over side $AB$
$E_b$ is the reflection of $M_a$ over side $AB$
the side-lengths satisfy equation (1)
the chord $F_cM_c$ is a diameter of the nine-point circle

Task

(Early seventies) In a non-right triangle , let be the side-lengths, the altitudes, the feet of the altitudes from the respective vertices, the midpoints of sides , the Euler points, the circumradius, the circumcenter, the nine-point center, the orthocenter, the reflection of over side , the reflection of over side , and the reflection of over side . PROVE that the following seventy-two statements are equivalent:
1. $E_c=F_c$
2. $AH=b$
3. $BH=a$
4. $AE_a=\frac{b}{2}$
5. $BE_b=\frac{a}{2}$
6. $OO^a=b$
7. $OO^b=a$
8. $CH=2h_c$
9. $h_a=AF_b$
10. $h_b=BF_a$
11. $AF_c=\frac{b^2}{2R}$
12. $BF_c=\frac{a^2}{2R}$
13. $\frac{a}{c} =\frac{h_c}{AF_b}$
14. $\frac{b}{c}=\frac{h_c}{BF_a}$
15. $\frac{a}{b}=\frac{BF_a}{AF_b}$
16. $R=\frac{b^2-a^2}{2c}$
17. $h_c=R\cos C$
18. $\cos A=\frac{b}{\sqrt{a^2+b^2}}$
19. $\cos B=-\frac{a}{\sqrt{a^2+b^2}}$
20. $\cos C=\frac{2ab}{a^2+b^2}$
21. $\sin A=\frac{a}{\sqrt{a^2+b^2}}$
22. $\sin B=\frac{b}{\sqrt{a^2+b^2}}$
23. $\sin C=\frac{b^2-a^2}{a^2+b^2}$
24. $\cos^2 A+\cos^2 B=1$
25. $\sin^2 A+\sin^2 B=1$
26. $a\cos A+b\cos B=0$
27. $\sin A+\cos B=0$
28. $\cos A-\sin B=0$
29. $2\cos A\cos B+\cos C=0$
30. $2\sin A\sin B-\cos C=0$
31. $\cos A\cos B+\sin A\sin B=0$
32. $a\cos A-b\cos B=\sqrt{a^2+b^2}\cos C$
33. $\sin A\sin B=\frac{ab}{b^2-a^2}\sin C$
34. $\sin^2B-\sin^2A=\sin C$
35. $\cos^2A-\cos^2B=\sin C$
36. $OH^2=5R^2-c^2$
37. $h_a^2+h_b^2=AB^2$
38. $\frac{h_a}{a}+\frac{h_b}{b}=\frac{c}{h_c}$
39. $a^2+b^2=4R^2$
40. $\left(c+2AF_c\right)^2=a^2+b^2$ or $\left(c+2BF_c\right)^2=a^2+b^2$
41. $A-B=\pm 90^{\circ}$
42. $(a^2-b^2)^2=(ac)^2+(cb)^2$
43. $AH^2+BH^2+CH^2=8R^2-c^2$
44. $b=2R\cos A$
45. $E_a$ is the reflection of $M_b$ over side $AB$
46. $E_b$ is the reflection of $M_a$ over side $AB$
47. $\triangle ABH$ is congruent to $\triangle ABC$
48. $\triangle OO^aO^b$ is congruent to $\triangle ABC$
49. $\triangle CNO$ is isosceles with $CN=NO$
50. $\triangle CNH$ is isosceles with $CN=NH$
51. $\triangle CHO$ is right angled at $C$
52. $N$ is the circumcenter of $\triangle CHO$
53. $\triangle O^cOC$ is right-angled at $O$
54. $\triangle O^cHC$ is right-angled at $H$
55. quadrilateral $O^cOHC$ is a rectangle
56. the points $O^c,O,C,H$ are concyclic with $OH$ as diameter
57. the reflection $O^b$ of $O$ over $AC$ lies internally on $AB$
58. the reflection $O^a$ of $O$ over $BC$ lies externally on $AB$
59. radius $OC$ is parallel to side $AB$
60. $F_a$ is the reflection of $F_b$ over side $AB$
61. the nine-point center lies on $AB$
62. the orthic triangle is isosceles with $F_aF_c=F_bF_c$
63. the geometric mean theorem holds
64. the bisector of $\angle C$ has length $l$ , where $l^2=\frac{2a^2b^2}{a^2+b^2}$
65. the orthocenter is a reflection of vertex $C$ over side $AB$
66. segment $HC$ is tangent to the circumcircle at point $C$
67. median $CM_c$ has the same length as the segment $HM_c$
68. the bisector $M_cO$ of $AB$ is tangent to the nine-point circle at $M_c$
69. $AF_aBF_b$ is a convex kite with diagonals $AB$ and $F_aF_b$
70. altitude $CF_c$ is tangent to the nine-point circle at $F_c$
71. chord $F_cM_c$ is a diameter of the nine-point circle
72. segment $HF_c$ is tangent to the nine-point circle at $F_c$ .
  ( $3$ short of the target.)
(Extra feature) If $\triangle ABC$ satisfies equation (??), PROVE that its nine-point center $N$ divides $AB$ in the ratio $|3b^2-a^2|:|b^2-3a^2|$ .