Use similar triangles.
This is the converse of the previous statement in example 1. One proof of it uses similar triangles and the law of sines.

By example 1 we have that ![]() . If
. If ![]() bisects
bisects ![]() , then
, then ![]() . And so
. And so ![]() . Similarly for the converse.
. Similarly for the converse.
By example 1 we have that ![]() . If
. If ![]() bisects
bisects ![]() , then
, then ![]() . And so
. And so ![]() . Similarly for the converse.
. Similarly for the converse.
This follows from example 3 and example 4 above, since ![]() and
and ![]() yield
yield ![]() and
and ![]() .
.
Brief relief
Takeaway
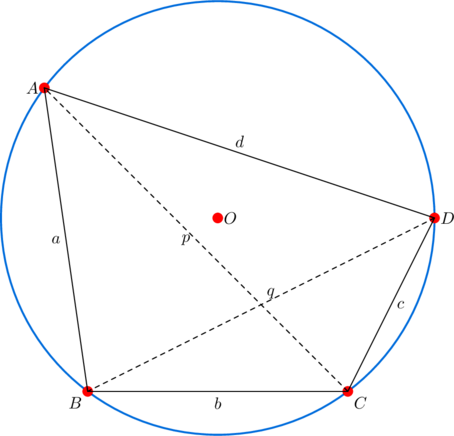
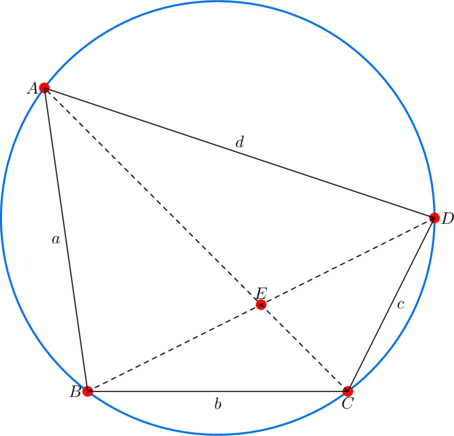
Let ![]() be a convex cyclic quadrilateral. Then the following statements are equivalent:
be a convex cyclic quadrilateral. Then the following statements are equivalent:
 is a rectangle
is a rectangle- diagonals
 and
and  bisect each other.
bisect each other.
Task
- (Easy verification) Let
 be a convex cyclic quadrilateral with vertices at
be a convex cyclic quadrilateral with vertices at  ,
,  ,
,  ,
,  . Verify that:
. Verify that:
- diagonal
 bisects diagonal
bisects diagonal 

 .
.
- diagonal