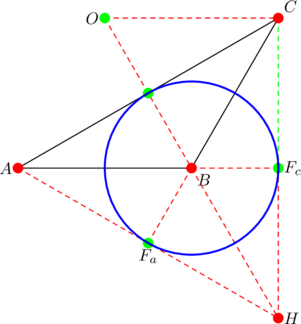
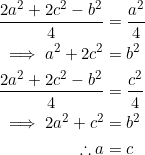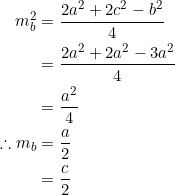If we now reflect vertex ![]() over side
over side ![]() we obtain the circumcenter.
we obtain the circumcenter.
It follows, in the case of the ![]() -triangle, that the reflection triangle is degenerate; in addition, it degenerates to a special line connecting the centroid, circumcenter and orthocenter, known as the Euler line.
-triangle, that the reflection triangle is degenerate; in addition, it degenerates to a special line connecting the centroid, circumcenter and orthocenter, known as the Euler line.
Is the ![]() -triangle the only triangle whose reflection triangle degenerates to the Euler line?
-triangle the only triangle whose reflection triangle degenerates to the Euler line?
To see how this holds, we’ll show that the length ![]() of the altitude through
of the altitude through ![]() is half the distance from
is half the distance from ![]() to the orthocenter
to the orthocenter ![]() . Indeed:
. Indeed:
![]()
and
![]()
This shows that the reflection of vertex ![]() over side
over side ![]() is the orthocenter
is the orthocenter ![]() .
.
Since ![]() , we have that
, we have that ![]() and
and ![]() . Thus, the reflection of vertex
. Thus, the reflection of vertex ![]() over side
over side ![]() is also the orthocenter.
is also the orthocenter.
To see this, note that since triangle ![]() is isosceles with
is isosceles with ![]() as the apex, the circumcenter lies on the axis of symmetry through
as the apex, the circumcenter lies on the axis of symmetry through ![]() . We just have to show that the radius through
. We just have to show that the radius through ![]() is twice the altitude through
is twice the altitude through ![]() . The altitude through
. The altitude through ![]() is:
is:
![]()
We’ve already seen this by explicitly determining the reflection triangle from the preceding three examples. Alternatively, the necessary and sufficient condition for a degenerate reflection triangle is ![]() . This condition holds in the case of the
. This condition holds in the case of the ![]() -triangle:
-triangle:
![]()
Let ![]() be the circumradius of the triangle. If the reflection of vertex
be the circumradius of the triangle. If the reflection of vertex ![]() over side
over side ![]() is the orthocenter, then we must have
is the orthocenter, then we must have ![]() , as per the equivalent statements here. Similarly, if the reflection of vertex
, as per the equivalent statements here. Similarly, if the reflection of vertex ![]() over side
over side ![]() is the orthocenter, then we must have
is the orthocenter, then we must have ![]() . These two relations yield
. These two relations yield ![]() . Since
. Since ![]() is also equivalent to
is also equivalent to ![]() , we obtain
, we obtain ![]() . Thus, the triangle is the
. Thus, the triangle is the ![]() -triangle.
-triangle.
Takeaway
In any triangle ![]() , let
, let ![]() be the side-lengths,
be the side-lengths, ![]() the orthocenter,
the orthocenter, ![]() the circumcenter, and
the circumcenter, and ![]() the circumradius. Then the following statements are equivalent:
the circumradius. Then the following statements are equivalent:


- the reflection of
 over
over  is
is 
- the reflection of
 over
over  is
is  and the reflection of
and the reflection of  over
over  is
is 
Task
- (Aufbau) In triangle
 , let
, let  be the side-lengths,
be the side-lengths,  the circumradius,
the circumradius,  the circumcenter,
the circumcenter,  the nine-point center, and
the nine-point center, and  the orthocenter. PROVE that the following statements are equivalent:
the orthocenter. PROVE that the following statements are equivalent:



- the reflection of
 over
over  is
is 
- radius
 is parallel to side
is parallel to side  and radius
and radius  is parallel to side
is parallel to side 
- the reflection of
 over
over  is
is  and the reflection of
and the reflection of  over
over  is
is