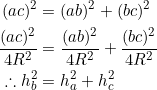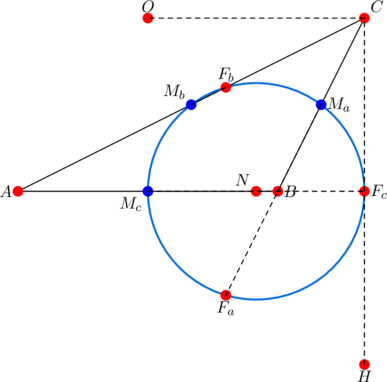
In the above diagram we have the nine-point circle of triangle ![]() going through the midpoints
going through the midpoints ![]() (of sides
(of sides ![]() respectively), and the feet of the altitudes
respectively), and the feet of the altitudes ![]() (from
(from ![]() in that order).
in that order).
(1) ![]()
if (and only if) the side-lengths ![]() satisfy
satisfy
(2) ![]()
It will also be shown, in our first example, that we have the relations
(3) 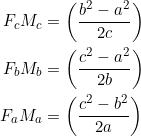
in any triangle (append absolute values if need be).
In the meantime, note that the right side of equation (1) evaluates to ![]() for a right triangle, where
for a right triangle, where ![]() is the circumradius, whereas both sides of equation (1) evaluate to
is the circumradius, whereas both sides of equation (1) evaluate to ![]() under (2). And so in the latter case, the segment
under (2). And so in the latter case, the segment ![]() is not just a chord, but a diameter of the nine-point circle.
is not just a chord, but a diameter of the nine-point circle.
Let’s do this for an acute triangle. Slight modification for an obtuse triangle will be needed. By drawing an appropriate diagram we have:
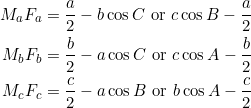
We can re-write the expression for ![]() entirely in terms of the side-lengths using the cosine formula:
entirely in terms of the side-lengths using the cosine formula:
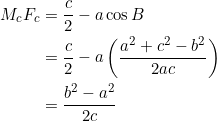
Similarly we obtain the expressions for ![]() and
and ![]() .
.
Since ![]() , we have
, we have ![]() by the usual notation. Using example 1 above we have
by the usual notation. Using example 1 above we have
![]()
and so ![]() .
.
We first have ![]() . Moreover, if
. Moreover, if ![]() is the circumradius, then
is the circumradius, then ![]() for a right triangle. Now:
for a right triangle. Now:
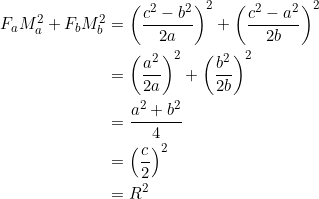
Such a triangle is necessarily non-right. Let ![]() be its circumradius. By one of the equivalent statements here, we know that equation (2) then becomes equivalent to
be its circumradius. By one of the equivalent statements here, we know that equation (2) then becomes equivalent to ![]() . Re-arrange equation (2) in the form
. Re-arrange equation (2) in the form ![]() and consider both sides of equation (1):
and consider both sides of equation (1):

By example 4 above, we had ![]() . Since the nine-point circle goes through
. Since the nine-point circle goes through ![]() and
and ![]() and has radius equal to
and has radius equal to ![]() , the fact that
, the fact that ![]() means that the chord
means that the chord ![]() is a diameter.
is a diameter.
No other triangle has this property.
Takeaway
In triangle ![]() , let
, let ![]() denote the Euler point of vertex
denote the Euler point of vertex ![]() ,
, ![]() the foot of the altitude from vertex
the foot of the altitude from vertex ![]() , and
, and ![]() the midpoint of side
the midpoint of side ![]() . Then the following statements are equivalent:
. Then the following statements are equivalent:
- the chord
 is a diameter of the nine-point circle
is a diameter of the nine-point circle  .
.
The equivalent conditions range from extremely simple to moderately involved.
Task
- (Late sixties) In a non-right triangle
 , let
, let  be the side-lengths,
be the side-lengths,  the altitudes,
the altitudes,  the feet of the altitudes from the respective vertices,
the feet of the altitudes from the respective vertices,  the midpoints of sides
the midpoints of sides  ,
,  the Euler points,
the Euler points,  the circumradius,
the circumradius,  the circumcenter,
the circumcenter,  the nine-point center,
the nine-point center,  the orthocenter,
the orthocenter,  the reflection of
the reflection of  over side
over side  ,
,  the reflection of
the reflection of  over side
over side  , and
, and  the reflection of
the reflection of  over side
over side  . PROVE that the following sixty-eight statements are equivalent:
. PROVE that the following sixty-eight statements are equivalent:





































 or
or 




 is congruent to
is congruent to 
 is congruent to
is congruent to 
 is isosceles with
is isosceles with 
 is isosceles with
is isosceles with 
 is right angled at
is right angled at 
 is the circumcenter of
is the circumcenter of 
 is right-angled at
is right-angled at 
 is right-angled at
is right-angled at 
- quadrilateral
 is a rectangle
is a rectangle - the points
 are concyclic with
are concyclic with  as diameter
as diameter - the reflection
 of
of  over
over  lies internally on
lies internally on 
- the reflection
 of
of  over
over  lies externally on
lies externally on 
- radius
 is parallel to side
is parallel to side 
 is the reflection of
is the reflection of  over side
over side 
- the nine-point center lies on

- the orthic triangle is isosceles with

- the geometric mean theorem holds
- the bisector of
 has length
has length  , where
, where 
- the orthocenter is a reflection of vertex
 over side
over side 
- segment
 is tangent to the circumcircle at point
is tangent to the circumcircle at point 
- median
 has the same length as the segment
has the same length as the segment 
- the bisector
 of
of  is tangent to the nine-point circle at
is tangent to the nine-point circle at 
 is a convex kite with diagonals
is a convex kite with diagonals  and
and 
- altitude
 is tangent to the nine-point circle at
is tangent to the nine-point circle at 
- chord
 is a diameter of the nine-point circle
is a diameter of the nine-point circle - segment
 is tangent to the nine-point circle at
is tangent to the nine-point circle at  .
.
( short of the target. Next target now is to extend the initial target.)
short of the target. Next target now is to extend the initial target.)
- (Extra feature) If
 satisfies equation (??), PROVE that its nine-point center
satisfies equation (??), PROVE that its nine-point center  divides
divides  in the ratio
in the ratio  .
.