A property of the Kepler triangle – High School Geometry

On May 14, 2021, we showed that the side-lengths $a,b,c$

( $b< a< c$

) of the Kepler triangle satisfy the identity

(1) $\begin{equation*} (ac)^2=(ab)^2+(bc)^2 \end{equation*}$

Or, in an upside-down form:

(2) $\begin{equation*} \frac{1}{b^2}=\frac{1}{a^2}+\frac{1}{c^2}\end{equation*}$

Of all right triangles, the Kepler triangle is the only one in which both the side-lengths and the reciprocals of the side-lengths satisfy Pythagorean identities.

On top of this, the Kepler triangle is also unique in that both the altitudes and the reciprocals of the altitudes satisfy Pythagorean identities.

(3) $\begin{equation*} h_b^2=h_a^2+h_c^2 \end{equation*}$

(4) $\begin{equation*} \frac{1}{h_c^2}=\frac{1}{h_a^2}+\frac{1}{h_b^2} \end{equation*}$

(Only the Kepler triangle satisfies equation (3) above, but other right triangles satisfy equation (4).)

PROVE that equations (1) and (2) are equivalent.

Our very first example of 2022 is a breeze. To see that (1) $\implies$ (2), re-arrange

$(ac)^2=(ab)^2+(bc)^2=b^2(a^2+c^2)\implies \frac{1}{b^2}=\frac{a^2+c^2}{(ac)^2}=\frac{1}{a^2}+\frac{1}{c^2}$

On the other hand, (2) $\implies$ (1) because

$\frac{1}{b^2}=\frac{1}{a^2}+\frac{1}{c^2}=\frac{a^2+c^2}{(ac)^2}\implies (ac)^2=b^2(a^2+c^2)=(ab)^2+(bc)^2$

PROVE that every right triangle satisfies equation (4).

Let $R$ be the radius of the circumcircle of any triangle $ABC$ with side-lengths $a,b,c$ . Then the altitudes $h_a,h_b,h_c$ from vertices $A,B,C$ are given by

$h_a=\frac{bc}{2R},h_b=\frac{ac}{2R},~h_c=\frac{ab}{2R}$

In the case of a right triangle with hypotenuse $c$ we have $c=2R$ and so $h_a=b,h_b=a,h_c=\frac{ab}{c}$ .

$\therefore\frac{1}{h_c^2}=\frac{c^2}{(ab)^2}=\frac{a^2+b^2}{(ab)^2}=\frac{1}{b^2}+\frac{1}{a^2}=\frac{1}{h_a^2}+\frac{1}{h_b^2}.$

PROVE that equation (3) implies equation (1).

Since $h_a=\frac{bc}{2R},h_b=\frac{ac}{2R},~h_c=\frac{ab}{2R}$ , we have

$h_b^2=h_a^2+h_c^2\implies\left(\frac{ac}{2R}\right)^2=\left(\frac{bc}{2R}\right)^2 +\left(\frac{ab}{2R}\right)^2$

Clear the common denominator and it becomes clear that

$(ac)^2=(ab)^2+(bc)^2.$

PROVE that equation (1) implies equation (3).

Suppose that equation (1) holds, so that $(ac)^2=(ab)^2+(bc)^2$ . Divide through by $4R^2$ and use the expressions for the altitudes given in example 2.

$\begin{equation*} \begin{split} (ac)^2&=(ab)^2+(bc)^2\\ \frac{(ac)^2}{4R^2}&=\frac{(ab)^2}{4R^2}+\frac{(bc)^2}{4R^2}\\ \therefore h_b^2&=h_a^2+h_c^2 \end{split} \end{equation*}$

PROVE that a right triangle is precisely the Kepler triangle, if it satisfies equation (3).

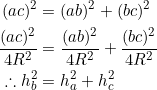
If a right triangle is of Kepler type, then by our post on May 14, 2021 , its side-lengths satisfy equation (1). By the preceding two examples, equations (1) and (3) are equivalent. Thus, a Kepler triangle satisfies equation (3).

Conversely, suppose that a right triangle with hypotenuse $c$ satisfies equation (3). Then $c^2=a^2+b^2$ and $(ac)^2=(ab)^2+(bc)^2$ . Multiply both sides of $c^2=a^2+b^2$ by $a^2$ to get $(ac)^2=a^4+(ab)^2$ . Now combine with $(ac)^2=(ab)^2+(bc)^2$ to get

$a^4=(bc)^2\implies a^2=bc$

In other words, the side-lengths $a,b,c$ form a geometric progression of the form $b,a,c$ . Thus, the right triangle is of the Kepler type.

Takeaway

Let $ABC$ be a (right) triangle whose side-lengths $a,b,c$ satisfy $c^2=a^2+b^2$ . Then the following statements are equivalent:

the sequence $b,a,c$ is geometric
$\frac{c}{b}$ is the golden ratio
$(ac)^2=(ab)^2+(bc)^2$
$\frac{1}{b^2}=\frac{1}{a^2}+\frac{1}{c^2}$
$\frac{1}{h_b^2}=\frac{1}{h_a^2}+\frac{1}{h_c^2}$ .

Such a triangle is the Kepler triangle.

Task

(Mid sixties) In a non-right triangle , let be the side-lengths, the altitudes, the feet of the altitudes from the respective vertices, the circumradius, the circumcenter, the nine-point center, the orthocenter, the midpoint of side , the reflection of over side , the reflection of over side , and the reflection of over side . PROVE that the following sixty-five statements are equivalent:
1. $AH=b$
2. $BH=a$
3. $OO^a=b$
4. $OO^b=a$
5. $CH=2h_C$
6. $h_A=AF_B$
7. $h_B=BF_A$
8. $AF_C=\frac{b^2}{2R}$
9. $BF_C=\frac{a^2}{2R}$
10. $\frac{a}{c} =\frac{h_C}{AF_B}$
11. $\frac{b}{c}=\frac{h_C}{BF_A}$
12. $\frac{a}{b}=\frac{BF_A}{AF_B}$
13. $R=\frac{b^2-a^2}{2c}$
14. $h_C=R\cos C$
15. $\cos A=\frac{b}{\sqrt{a^2+b^2}}$
16. $\cos B=-\frac{a}{\sqrt{a^2+b^2}}$
17. $\cos C=\frac{2ab}{a^2+b^2}$
18. $\sin A=\frac{a}{\sqrt{a^2+b^2}}$
19. $\sin B=\frac{b}{\sqrt{a^2+b^2}}$
20. $\sin C=\frac{b^2-a^2}{a^2+b^2}$
21. $\cos^2 A+\cos^2 B=1$
22. $\sin^2 A+\sin^2 B=1$
23. $a\cos A+b\cos B=0$
24. $\sin A+\cos B=0$
25. $\cos A-\sin B=0$
26. $2\cos A\cos B+\cos C=0$
27. $2\sin A\sin B-\cos C=0$
28. $\cos A\cos B+\sin A\sin B=0$
29. $a\cos A-b\cos B=\sqrt{a^2+b^2}\cos C$
30. $\sin A\sin B=\frac{ab}{b^2-a^2}\sin C$
31. $\sin^2B-\sin^2A=\sin C$
32. $OH^2=5R^2-c^2$
33. $h_A^2+h_B^2=AB^2$
34. $\frac{h_A}{a}+\frac{h_B}{b}=\frac{c}{h_C}$
35. $a^2+b^2=4R^2$
36. $\left(c+2AF_C\right)^2=a^2+b^2$ or $\left(c+2BF_C\right)^2=a^2+b^2$
37. $A-B=\pm 90^{\circ}$
38. $(a^2-b^2)^2=(ac)^2+(cb)^2$
39. $AH^2+BH^2+CH^2=8R^2-c^2$
40. $b=2R\cos A$
41. $\triangle ABH$ is congruent to $\triangle ABC$
42. $\triangle OO^aO^b$ is congruent to $\triangle ABC$
43. $\triangle CNO$ is isosceles with $CN=NO$
44. $\triangle CNH$ is isosceles with $CN=NH$
45. $\triangle CHO$ is right angled at $C$
46. $N$ is the circumcenter of $\triangle CHO$
47. $\triangle O^cOC$ is right-angled at $O$
48. $\triangle O^cHC$ is right-angled at $H$
49. quadrilateral $O^cOHC$ is a rectangle
50. the points $O^c,O,C,H$ are concyclic with $OH$ as diameter
51. the reflection $O^b$ of $O$ over $AC$ lies internally on $AB$
52. the reflection $O^a$ of $O$ over $BC$ lies externally on $AB$
53. radius $OC$ is parallel to side $AB$
54. $F_A$ is the reflection of $F_B$ over side $AB$
55. the nine-point center lies on $AB$
56. the orthic triangle is isosceles with $F_AF_C=F_BF_C$
57. the geometric mean theorem holds
58. the bisector of $\angle C$ has length $l$ , where $l^2=\frac{2a^2b^2}{a^2+b^2}$
59. the orthocenter is a reflection of vertex $C$ over side $AB$
60. segment $HC$ is tangent to the circumcircle at point $C$
61. median $CM$ has the same length as the segment $HM$
62. the bisector $MO$ of $AB$ is tangent to the nine-point circle at $M$
63. $AF_ABF_B$ is a convex kite with diagonals $AB$ and $F_AF_B$
64. altitude $CF_C$ is tangent to the nine-point circle at $F_C$
65. segment $HF_C$ is tangent to the nine-point circle at $F_C$ .
  ( $10$ short of the target.)
(Extra feature) If $\triangle ABC$ satisfies equation (??), PROVE that its nine-point center $N$ divides $AB$ in the ratio $|3b^2-a^2|:|b^2-3a^2|$ .