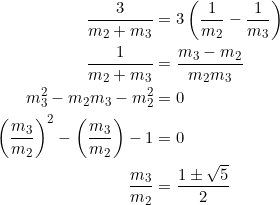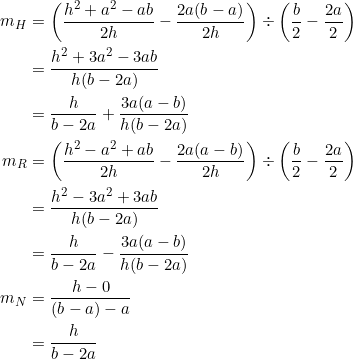Anyone who’s taken a stat course before may inadvertently misconstrue the title as “mean, median, mode” — and thereby get a slight shock, because we actually called “mean median slope”. After one recovers from this shock, one discovers that this post covers a leftover from our first post in this October. There, we went over some things hurriedly, which made this carryover necessary.
Excursion
As we hit the road, have your pencil, paper, and patience ready.
Find the slopes of the three medians of ![]() with vertices at
with vertices at ![]() ,
, ![]() ,
, ![]() .
.
The midpoints of sides ![]() ,
, ![]() , and
, and ![]() are
are ![]() ,
, ![]() , and
, and ![]() , respectively. Thus, the slopes of the medians are:
, respectively. Thus, the slopes of the medians are:
![]()
What do you notice about the reciprocals ![]() ?
?
Find the slopes of the three medians of ![]() with vertices at
with vertices at ![]() ,
, ![]() ,
, ![]() .
.
The midpoints of sides ![]() are
are ![]() ,
, ![]() ,
, ![]() , respectively. Thus, the slopes of the medians are:
, respectively. Thus, the slopes of the medians are:
![]()
Re-arrange them as ![]() . What do you notice?
. What do you notice?
PROVE that if a triangle has one side parallel to the ![]() -axis, then the reciprocals of the slopes of the three medians form an arithmetic progression.
-axis, then the reciprocals of the slopes of the three medians form an arithmetic progression.
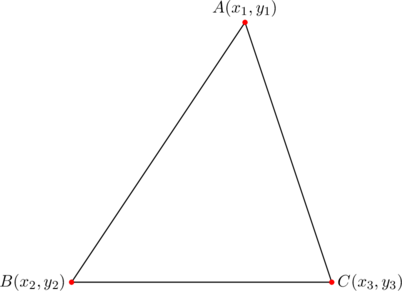
In the above diagram, let’s require that ![]() , so that side
, so that side ![]() is parallel to the
is parallel to the ![]() -axis.
-axis.
Normally, the slopes of the medians from vertices ![]() are:
are:
![]()
If we now put ![]() and consider the reciprocals
and consider the reciprocals
![]()
then
![]()
Thus, the reciprocals ![]() of the median slopes form an arithmetic progression, and the arithmetic mean of this progression is the slope of the median from the vertex opposite the side parallel to the
of the median slopes form an arithmetic progression, and the arithmetic mean of this progression is the slope of the median from the vertex opposite the side parallel to the ![]() -axis.
-axis.
In the special case when ![]() , we have that the median from vertex
, we have that the median from vertex ![]() is vertical, and so its slope is undefined. Nevertheless, since we’re concerned with the reciprocals of the slopes, the conclusion still holds. In fact, we obtain a special arithmetic progression
is vertical, and so its slope is undefined. Nevertheless, since we’re concerned with the reciprocals of the slopes, the conclusion still holds. In fact, we obtain a special arithmetic progression ![]() , where
, where ![]() .
.
Express the common difference of the arithmetic progression in the previous example in terms of the slopes of the parent triangle.
The arithmetic progression is ![]() . The common difference is the difference between consecutive terms; for example,
. The common difference is the difference between consecutive terms; for example, ![]() :
:
(1) 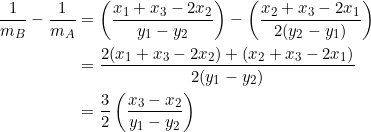
Consider the difference between the reciprocals of the slopes of sides ![]() and
and ![]() :
:
(2) 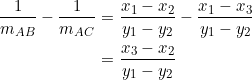
It follows from (1) and (2) that ![]() .
.
converse results: click to read
The converse of example 3 and example 5 below will be shown in example 9 and example 8.
clockwise rotation: click to read
Having established the two preceding examples, the next two can be proved using rotations — specifically, a ninety degree (clockwise or counter-clockwise) rotation about a convenient center. Nevertheless, we’ll still use a direct method.
PROVE that if a triangle has one side parallel to the ![]() -axis, then the slopes of the three medians form an arithmetic progression.
-axis, then the slopes of the three medians form an arithmetic progression.
Let the vertices be placed at ![]() ,
, ![]() ,
, ![]() . Here, side
. Here, side ![]() is parallel to the
is parallel to the ![]() -axis. The slopes of the three medians are:
-axis. The slopes of the three medians are:
![]()
and so
![]()
Easy stuff.
Express the common difference of the arithmetic progression in the previous example in terms of the slopes of the parent triangle.
Let the common difference be ![]() . Using the median slopes in the preceding example, we have:
. Using the median slopes in the preceding example, we have:
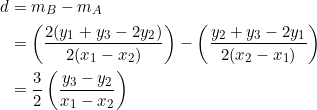
Consider the difference between the slopes of sides ![]() and
and ![]() :
:
![]()
Thus, ![]() .
.
Exception
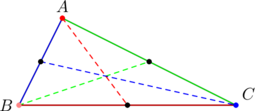
In fact, exceptional. In the case of a right triangle with legs parallel to the coordinate axes, something interesting happens.
PROVE that if a right triangle has legs parallel to the coordinate axes, then the slopes of the three medians form a geometric progression with ![]() , and when re-arranged, form an arithmetic progression.
, and when re-arranged, form an arithmetic progression.
Suppose the situation is pictured below:
and let’s apply, as an informal argument, an exercise from our immediate past post. That exercise says that if ![]() form an arithmetic progression and at the same time the reciprocals
form an arithmetic progression and at the same time the reciprocals ![]() form another arithmetic progression (in the same order), then the relation
form another arithmetic progression (in the same order), then the relation ![]() holds — which is a condition for
holds — which is a condition for ![]() to be a geometric progression.
to be a geometric progression.
In the present case, because side ![]() is parallel to the
is parallel to the ![]() -axis, we have (by example 3) that the reciprocals
-axis, we have (by example 3) that the reciprocals ![]() of the median slopes form an arithmetic progression. Similarly, since side
of the median slopes form an arithmetic progression. Similarly, since side ![]() is parallel to the
is parallel to the ![]() -axis, we have (by example 5) that the median slopes
-axis, we have (by example 5) that the median slopes ![]() form an arithmetic progression. Together, we arrive at a scenario described in the previous paragraph. This sheds a little light on why the median slopes behave specially in this case.
form an arithmetic progression. Together, we arrive at a scenario described in the previous paragraph. This sheds a little light on why the median slopes behave specially in this case.
We can continue this informal argument to show that the common ratio of the geometric progression is ![]() , but there’s a simpler, more direct alternative:
, but there’s a simpler, more direct alternative:
![]()
The geometric progression is ![]() and the common ratio is
and the common ratio is ![]() . At the same time, we have an arithmetic progression
. At the same time, we have an arithmetic progression ![]() because
because ![]() .
.
Extensions
Suppose that the slopes of the medians of ![]() form an arithmetic progression
form an arithmetic progression ![]() with common difference
with common difference ![]() . PROVE that side
. PROVE that side ![]() is parallel to the
is parallel to the ![]() -axis.
-axis.
As you’ll notice, this is the converse of example 5. The proof is simple, but involves some algebraic manipulations. So we present a snapshot below.
Let the vertices be ![]() ,
, ![]() ,
, ![]() . Since
. Since ![]() , we have:
, we have:
(3) ![]()
After some simplifications, this reduces to:
![]()
The expression in the first square bracket, namely
![]()
cannot be zero (it actually represents twice the triangle area). This forces
(4) ![]()
(5) ![]()
Simplifying, we obtain
![]()
(6) ![]()
![]()
Thus, ![]() , showing that side
, showing that side ![]() is parallel to the
is parallel to the ![]() -axis.
-axis.
Suppose that the reciprocals of the slopes of the medians of ![]() form an arithmetic progression
form an arithmetic progression ![]() with common difference
with common difference ![]() . PROVE that side
. PROVE that side ![]() is parallel to the
is parallel to the ![]() -axis.
-axis.
Because the proof is similar to the previous one, we omit it. Just take our word for its validity; better still, try it as an activity.
Consider two right triangles in which the legs have the same slopes, but the hypotenuse of one is parallel to the ![]() -axis, while the hypotenuse of the other is parallel to the
-axis, while the hypotenuse of the other is parallel to the ![]() -axis. PROVE that in both cases, the common differences of the arithmetic progressions formed by the slopes of the medians are equal.
-axis. PROVE that in both cases, the common differences of the arithmetic progressions formed by the slopes of the medians are equal.
One may think that this has something to do with similarity, but it’s more than that.
The reason it happens is simple. In example 4, the common difference of the reciprocals of the median slopes when one side is parallel to the ![]() -axis was given by
-axis was given by
![]()
In In example 6, the common difference of the median slopes when one side is parallel to the ![]() -axis was
-axis was
![]()
If these two common differences should be equal, then
![]()
So the triangle must be a right triangle. Similarity is not enough. To see this, consider ![]() with vertices at
with vertices at ![]() ,
, ![]() ,
, ![]() . The reciprocals of the slopes of the three medians are:
. The reciprocals of the slopes of the three medians are:
![]()
Now consider ![]() with vertices at
with vertices at ![]() ,
, ![]() ,
, ![]() . Notice that
. Notice that ![]() is similar to
is similar to ![]() . However, the slopes of the three medians of
. However, the slopes of the three medians of ![]() are
are
![]()
Takeaway
For any ![]() , the following two conditions are equivalent:
, the following two conditions are equivalent:
- side
 is parallel to the
is parallel to the  -axis;
-axis; - the reciprocals of the median slopes form an arithmetic progression
 ,
,  ,
,  with common difference
with common difference  .
.
Similarly, the following two conditions are equivalent for any ![]() :
:
- side
 is parallel to the
is parallel to the  -axis;
-axis; - the median slopes form an arithmetic progression
 ,
,  ,
,  with common difference
with common difference  .
.
Beautiful, simple things.
Tasks
- (Isosixless triangle) Let
 be isosceles such that
be isosceles such that  .
.
- if the base
 is parallel to the
is parallel to the  -axis, PROVE that
-axis, PROVE that  ;
; - if the base
 is parallel to the
is parallel to the  -axis, PROVE that
-axis, PROVE that  .
.
(Beautiful scenes. More in exercise 2 below.)
- if the base
- (Isosixless triangle) Consider
 with vertices at
with vertices at  ,
,  ,
,  , where
, where  . (Side
. (Side  is parallel to the
is parallel to the  -axis.)
-axis.)
- PROVE that
 .
. - Deduce that
 if, and only if,
if, and only if,  .
.
(Among all triangles with one side parallel to the -axis, only the isosceles triangle has the property that
-axis, only the isosceles triangle has the property that  . Hence the name isosixless.)
. Hence the name isosixless.)
- PROVE that
- (Equilateral triangle) Let
 be equilateral with side-slopes
be equilateral with side-slopes  ,
,  ,
,  and median-slopes
and median-slopes  ,
,  ,
,  .
.
- PROVE that
 .
. - Using the above and exercise 1, deduce that if side
 is parallel to the
is parallel to the  -axis, then the slopes of the other two sides are
-axis, then the slopes of the other two sides are  .
. - PROVE that the side-slopes form an arithmetic progression if, and only if,

- PROVE that the side-slopes form a geometric progression if, and only if,

(Beautiful scenes.)
- PROVE that
- Verify that the solutions to the polynomial equation
 are
are  ,
,  ,
,  .
. - (Reversible sequence) PROVE that any three-term geometric progression with common ratio
 can always be re-arranged to form a three-term arithmetic progression.
can always be re-arranged to form a three-term arithmetic progression. - Let
 be distinct numbers and suppose that
be distinct numbers and suppose that  form an arithmetic sequence while
form an arithmetic sequence while  form a geometric sequence. PROVE that the common ratio of the geometric sequence is necessarily
form a geometric sequence. PROVE that the common ratio of the geometric sequence is necessarily  . (Compare with the preceding exercise.)
. (Compare with the preceding exercise.) - Let
 ,
,  , and
, and  denote the slopes of medians from vertices
denote the slopes of medians from vertices  ,
,  , and
, and  . Find a triangle for which the following three relations hold simultaneously:
. Find a triangle for which the following three relations hold simultaneously:
-
 ;
;  ;
; . (Implied by the first two.)
. (Implied by the first two.)
-
- If the “base”
 of an isosceles triangle
of an isosceles triangle  is parallel to the
is parallel to the  -axis, PROVE that the slopes of the two equal sides are opposites of each other. Thus, the side-slopes will form an arithmetic progression of the form
-axis, PROVE that the slopes of the two equal sides are opposites of each other. Thus, the side-slopes will form an arithmetic progression of the form  . Furthermore, PROVE that:
. Furthermore, PROVE that:

 .
.
(If the “base” of an isosceles triangle is parallel to the -axis, the slopes of the three medians form an arithmetic progression of the form
-axis, the slopes of the three medians form an arithmetic progression of the form  .)
.)
- Consider
 with vertices at
with vertices at  ,
,  ,
,  , where
, where  is fixed.
is fixed.
- Verify that the median slopes are
 ,
,  ,
,  , and that they form an arithmetic progression
, and that they form an arithmetic progression  with common difference
with common difference  .
.
(It’s somewhat interesting that this common difference stays the same as varies.)
varies.) - Find the value of
 for which the arithmetic sequence above becomes a geometric sequence with common ratio
for which the arithmetic sequence above becomes a geometric sequence with common ratio  .
.
- Verify that the median slopes are
- Find coordinates for the vertices of
 in which:
in which:
- the slopes of the three medians are
 .
. - the slopes of the three medians are
 .
. - the slopes of the three medians are
 .
. - the slopes of the three medians are
 .
. - the slopes of the three medians are
 .
.
(Since the median slopes form an arithmetic progression with common difference
 , one can use the preceding exercise and just substitute suitable values of
, one can use the preceding exercise and just substitute suitable values of  . However, there other possibilities and procedures that yield the same results.)
. However, there other possibilities and procedures that yield the same results.) - the slopes of the three medians are