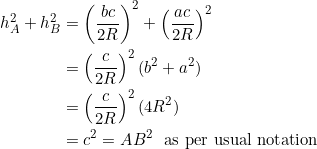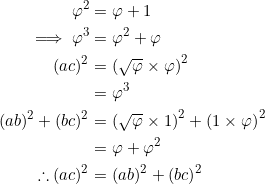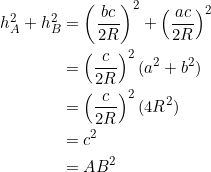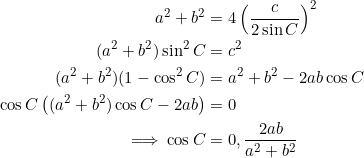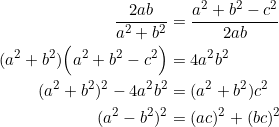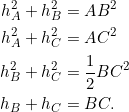(1) 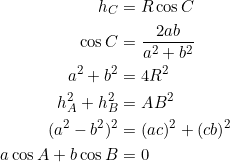
implies the others. Further, under this equivalence, the orthic triangle of the parent triangle is necessarily isosceles.
Obvious things
Observe that ![]() , and so a triangle that satisfies the entire chain of equivalence in (1) cannot be equilateral. Also, a right triangle with hypotenuse
, and so a triangle that satisfies the entire chain of equivalence in (1) cannot be equilateral. Also, a right triangle with hypotenuse ![]() satisfies both
satisfies both ![]() and
and ![]() , but not the rest. Hence, the non-right triangle requirement is essential.
, but not the rest. Hence, the non-right triangle requirement is essential.
Obtuse triangle
As the post’s title gives away, the first obvious thing to get out of the way.
This is evident from ![]() .
.
Other techniques
Alternatively, one can compute the cosine of ![]() or
or ![]() explicitly, using
explicitly, using ![]() and the cosine formula:
and the cosine formula:
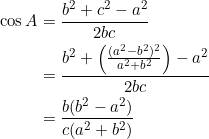
Similarly, ![]() . Now
. Now ![]() implies either
implies either ![]() or
or ![]() . In turn, either
. In turn, either ![]() or
or ![]() , showing that one of the two angles
, showing that one of the two angles ![]() is obtuse.
is obtuse.
Oversimple theorem
Now, let’s attempt to make our simple equivalence even simpler by splitting the proof into six parts.
From ![]() , isolate
, isolate ![]() and then use the fact that
and then use the fact that ![]() :
:
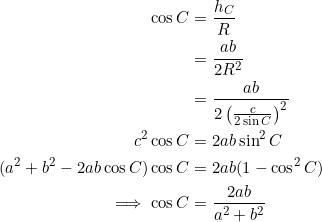
By the extended law of sines, we have ![]() . So:
. So:
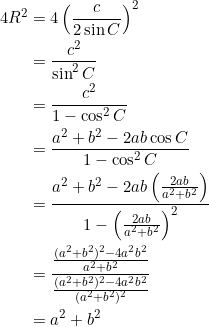
From ![]() , we have:
, we have:

Since we’re in a non-right triangle setting, we choose ![]() . Then compute
. Then compute ![]() :
:
![]()
From ![]() , isolate
, isolate ![]() . Then:
. Then:
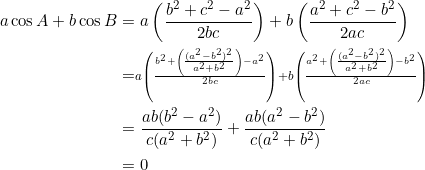
Note that ![]() gives
gives ![]() . So:
. So:
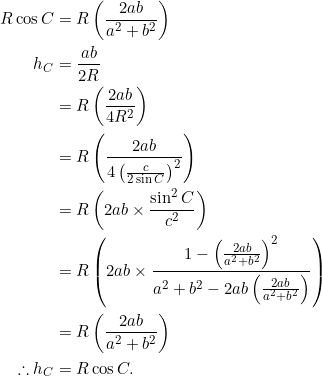
Six. Perfect.
Orthic triangle
The triangle obtained by joining the feet of the three altitudes of a parent triangle is called its orthic triangle.
The lengths of the sides of an orthic triangle are given by ![]() ,
, ![]() ,
, ![]() (one of these may require an absolute value if the parent triangle is obtuse). One of our equivalent statements is
(one of these may require an absolute value if the parent triangle is obtuse). One of our equivalent statements is ![]() . Thus, the orthic triangle has two sides equal. And we can even make it three.
. Thus, the orthic triangle has two sides equal. And we can even make it three.
First suppose that ![]() . Using the cosine formula:
. Using the cosine formula:
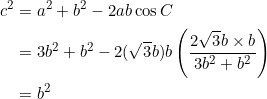
Thus, ![]() . Next, suppose that the parent triangle is isosceles with
. Next, suppose that the parent triangle is isosceles with ![]() . We’ll show that its orthic triangle is equilateral. Indeed, we already had
. We’ll show that its orthic triangle is equilateral. Indeed, we already had ![]() . It now suffices to show that
. It now suffices to show that ![]() . By the cosine formula:
. By the cosine formula:
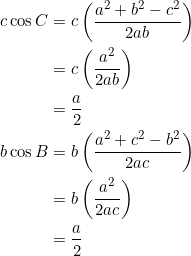
Thus, the orthic triangle is equilateral. Finally, suppose that the orthic triangle is equilateral. Consider ![]() :
:
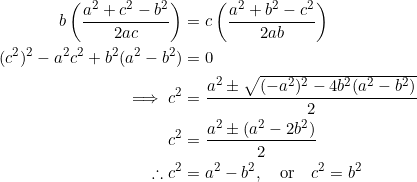
Discard ![]() since we’re dealing with a non-right triangle. The second possibility then yields
since we’re dealing with a non-right triangle. The second possibility then yields ![]() . Now use
. Now use ![]() in the equation
in the equation ![]() :
:
![]()
All this trouble just for a single triangle: the one in which ![]() ,
, ![]() ,
, ![]() . That’s the triangle that satisfies the equivalent conditions just established.
. That’s the triangle that satisfies the equivalent conditions just established.
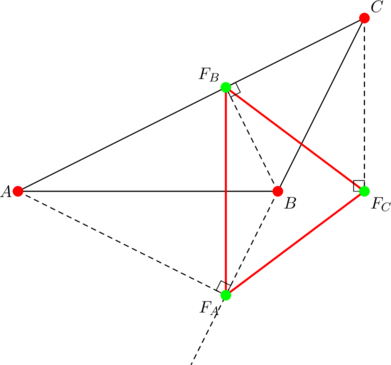
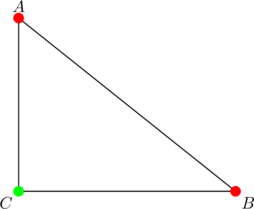
The feet of the altitudes from ![]() are
are ![]() ,
, ![]() , and
, and ![]() , as shown above. By the distance formula:
, as shown above. By the distance formula:
![]()
Notice that the foot of the altitude from ![]() coincides with our favourite point
coincides with our favourite point ![]() .
.
Takeaway
For any non-right triangle ![]() satisfying the chain of equivalence in (1), the three statements below are equivalent:
satisfying the chain of equivalence in (1), the three statements below are equivalent:


- the orthic triangle is equilateral.
Thus, there’s only “one” strictly isosceles triangle whose orthic triangle is equilateral.
Tasks
- Let
 be the interior angles of a triangle
be the interior angles of a triangle  , and let
, and let  be the side-lengths. Relative to these measurements, PROVE that:
be the side-lengths. Relative to these measurements, PROVE that:
- the interior angles of the orthic triangle are
 ,
,  ,
,  , if the parent triangle is acute
, if the parent triangle is acute - the interior angles of the orthic triangle are
 ,
,  ,
,  , if the parent triangle contains an obtuse angle
, if the parent triangle contains an obtuse angle 
- the side-lengths of the orthic triangle are
 ,
,  ,
,  (one of these will be negative if the parent triangle contains an obtuse angle, in which case an absolute value will be needed).
(one of these will be negative if the parent triangle contains an obtuse angle, in which case an absolute value will be needed).
- the interior angles of the orthic triangle are
- Let
 be a real number. Consider
be a real number. Consider  with interior angles
with interior angles  ,
,  , and
, and  .
.
- What restrictions, if any, must be imposed on
 ?
? - PROVE that the orthic triangle associated with
 is isosceles.
is isosceles.
- What restrictions, if any, must be imposed on
- PROVE that the two statements below are equivalent for a triangle
 :
:
 and
and 
 ,
,  ,
,  .
.
- Consider
 with vertices at
with vertices at  ,
,  ,
,  . Find:
. Find:
- the coordinates of the feet of the three altitudes
- the lengths of the sides of the orthic triangle
- a condition for which the orthic triangle will be equilateral.
- PROVE that the following statements are equivalent for any triangle:
- the orthic triangle is equilateral
- the parent triangle is equilateral or the parent triangle is isosceles with base angles of
 and an apex angle of
and an apex angle of  .
.