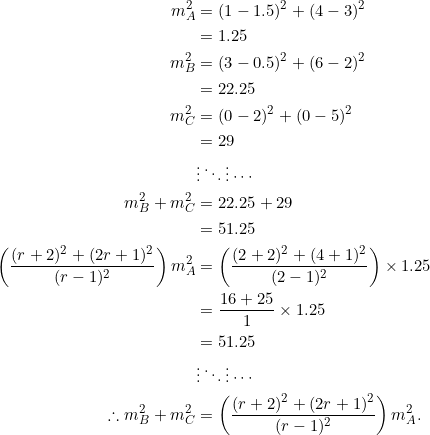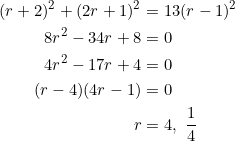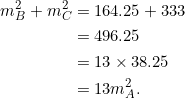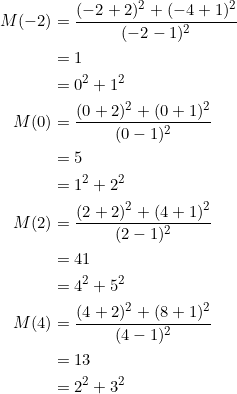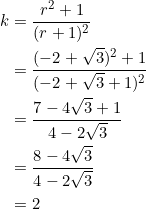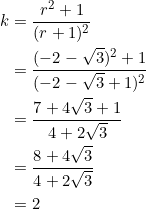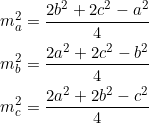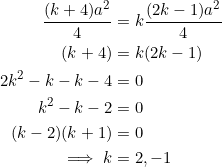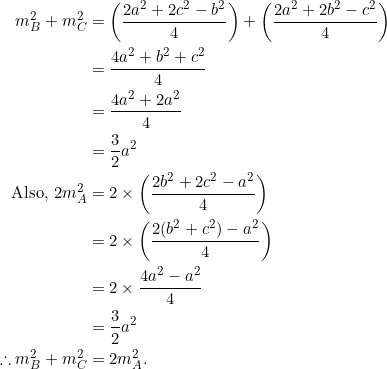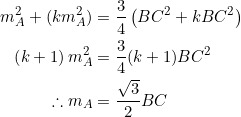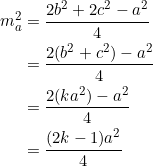The chances that you’ve seen the quadratic equations
(1) ![]()
(2) ![]()
are not slim. We now show you that they spring from familiar scenes.
Equilateral triangles
Example
If the slopes of the sides of an equilateral triangle are ![]() , PROVE that
, PROVE that ![]() .
.
In a previous post we showed that the side lengths ![]() of any triangle with slopes
of any triangle with slopes ![]() are related via
are related via
(3) ![]()
In the case of an equilateral triangle we put ![]() in (3) and obtain
in (3) and obtain
![]()
from which ![]() follows after simplification.
follows after simplification.
That was too simple, aided by (3). Below we provide an alternate derivation.
Let ![]() be the common ratio of the slopes of the sides of an equilateral triangle, and let
be the common ratio of the slopes of the sides of an equilateral triangle, and let ![]() be the common ratio of the slopes of the medians. PROVE that
be the common ratio of the slopes of the medians. PROVE that ![]() .
.
To see this, first observe that if the slopes of the sides of a triangle are ![]() , then the slopes of the medians to these sides are
, then the slopes of the medians to these sides are
(4) ![]()
respectively. For an equilateral triangle, the three medians are perpendicular to the sides, so:
(5) 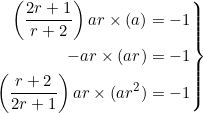
The first and third ones give ![]() . Divide by the common factor
. Divide by the common factor ![]() :
:
(6) ![]()
From (4), the common ratio ![]() for the slopes of the medians is
for the slopes of the medians is ![]() . Like so:
. Like so:
(7) ![]()
where ![]() is the original common ratio. Equation (6) may then be re-written as
is the original common ratio. Equation (6) may then be re-written as
![]()
Square roots: ![]() . We claim that
. We claim that ![]() is not possible. Otherwise, suppose we have
is not possible. Otherwise, suppose we have ![]() . Use the fact that
. Use the fact that ![]() to obtain
to obtain ![]() .
.
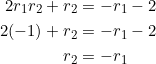
Now use ![]() and
and ![]() to get
to get ![]() , whence
, whence ![]() . From slope consideration, this is impossible for the common ratio of a geometric progression, and so
. From slope consideration, this is impossible for the common ratio of a geometric progression, and so ![]() ules out the possibility of
ules out the possibility of ![]() .
.
This forces ![]() .
.
While having ![]() is enough for what we want to achieve, it is important to point out that one can also have
is enough for what we want to achieve, it is important to point out that one can also have ![]() , depending on the arrangement of the geometric progressions. Hopefully this doesn’t cause any confusion.
, depending on the arrangement of the geometric progressions. Hopefully this doesn’t cause any confusion.
Let ![]() be the common ratio of the slopes of the sides of an equilateral triangle, and let
be the common ratio of the slopes of the sides of an equilateral triangle, and let ![]() be the common ratio of the slopes of the medians. PROVE that
be the common ratio of the slopes of the medians. PROVE that ![]() .
.
From the preceding example, ![]() . Use this in (7):
. Use this in (7):
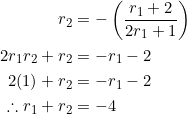
Simple.
Use examples 2 and 3 to deduce that in an equilateral triangle with side slopes ![]() , the quadratic equation
, the quadratic equation ![]() is satisfied by the common ratio of the slopes of the sides and the common ratio of the slopes of the medians.
is satisfied by the common ratio of the slopes of the sides and the common ratio of the slopes of the medians.
Since ![]() (view this as product of roots) and
(view this as product of roots) and ![]() (sum of roots), we get
(sum of roots), we get ![]() . Similarly,
. Similarly, ![]() .
.
Solve the quadratic equation ![]() and interpret the solution(s) in the context of equilateral triangles.
and interpret the solution(s) in the context of equilateral triangles.
The discriminant of the quadratic is ![]() . Since it is positive but not a perfect square, we expect two real, irrational solutions. By the quadratic formula:
. Since it is positive but not a perfect square, we expect two real, irrational solutions. By the quadratic formula:
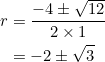
Should the slopes of the sides (and medians) of an equilateral triangle form a geometric progression, the common ratio of the progression is restricted to either ![]() or
or ![]() . Talk about
. Talk about ![]() est
est![]() ictions.
ictions.
Right isosceles triangles
If the slopes of the sides of a right isosceles triangle are ![]() , PROVE that
, PROVE that ![]() .
.
The side lengths ![]() will satisfy (3):
will satisfy (3):
![]()
where ![]() is the length of the side with slope
is the length of the side with slope ![]() ,
, ![]() is the length of the side with slope
is the length of the side with slope ![]() , and
, and ![]() is the length of the side with slope
is the length of the side with slope ![]() .
.
Since ![]() cannot be the hypotenuse, we’ll choose either
cannot be the hypotenuse, we’ll choose either ![]() or
or ![]() as the hypotenuse. To be specific, let
as the hypotenuse. To be specific, let ![]() be the hypotenuse.
be the hypotenuse.
The isosceles condition then forces ![]() . And:
. And:
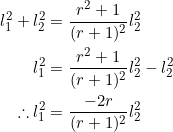
By the Pythagorean theorem, ![]() . As
. As ![]() , this yields
, this yields ![]() . Together with
. Together with ![]() , we obtain
, we obtain
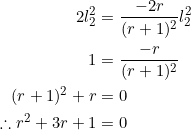
Solve the equation ![]() and interpret the solution(s) in relation to right isosceles triangles.
and interpret the solution(s) in relation to right isosceles triangles.
The discriminant is ![]() . Since the discriminant is positive but not a perfect square, we expect two real, irrational solutions.
. Since the discriminant is positive but not a perfect square, we expect two real, irrational solutions.
By the quadratic formula:
![]()
Should the slopes of the sides of a right isosceles triangle form a geometric progression, there are only two possible values for the common ratio of the progression, namely ![]() or
or ![]() .
.
Let ![]() be the slopes of the sides of a right isosceles triangle, with
be the slopes of the sides of a right isosceles triangle, with ![]() . PROVE that
. PROVE that ![]() .
.
The side with slope ![]() cannot be the hypotenuse. Let the hypotenuse be the side with slope
cannot be the hypotenuse. Let the hypotenuse be the side with slope ![]() . Then the slopes of the legs are
. Then the slopes of the legs are ![]() and
and ![]() . As such
. As such ![]() :
:
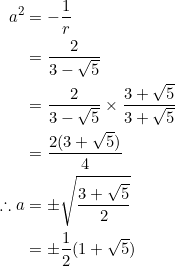
where ![]() was obtained by first setting
was obtained by first setting ![]() then squaring both sides to get
then squaring both sides to get ![]() , and then finally solving the linear-quadratic system
, and then finally solving the linear-quadratic system ![]() to get
to get ![]() ,
, ![]() (or
(or ![]() ,
, ![]() ).
).
Due to its connection to the golden ratio, we’ll have more to say about this example in a later post.
Let ![]() and
and ![]() . PROVE that
. PROVE that ![]() and
and ![]() .
.
By direct calculation:
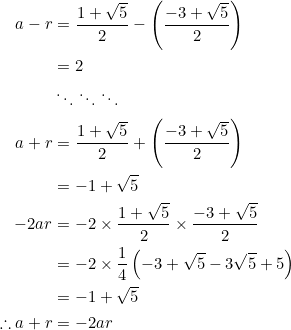
Of course, both ![]() and
and ![]() yield
yield ![]() .
.
Let ![]() and
and ![]() . PROVE that
. PROVE that ![]() and
and ![]()
As in the previous example, proceed by direct calculation:
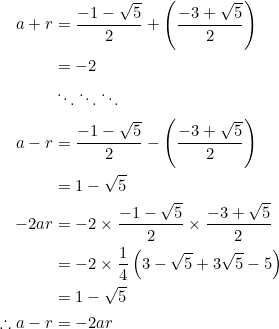
Several other nice relations exist between ![]() and
and ![]() .
.
Takeaway
At the level of slopes, equilateral triangles and right isosceles triangles are very close, as these equations show:
![]()
The slopes must form a geometric progression though.
Tasks
- (T w o nice) Let
 be the slopes of the sides of a triangle.
be the slopes of the sides of a triangle.
- If the triangle is equilateral, PROVE that the sum of product of the slopes, taken two slopes at a time, is always negative three. That is,
 ;
; - If the triangle is right isosceles, PROVE that the sum of product of the slopes, taken two slopes at a time, is always twice the common ratio. That is,
 .
.
- If the triangle is equilateral, PROVE that the sum of product of the slopes, taken two slopes at a time, is always negative three. That is,
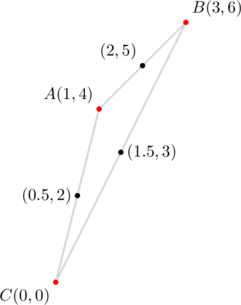
- In
 , suppose that the slopes of sides
, suppose that the slopes of sides  are
are  , respectively. PROVE that:
, respectively. PROVE that:
- the slope of the median from
 is
is  ;
; - the slope of the median from
 is
is  ;
; - the slope of the median from
 is
is  .
.
- the slope of the median from
- In
 , let
, let  be the slopes of sides
be the slopes of sides  , in that order.
, in that order.
- If
 , PROVE that
, PROVE that  (Use exercise 2 above together with the fact that the median from vertex
(Use exercise 2 above together with the fact that the median from vertex  to side
to side  is actually an altitude due to the fact that
is actually an altitude due to the fact that  );
); - If
 and
and  , deduce that
, deduce that  . (This provides another means of deriving equation (2).)
. (This provides another means of deriving equation (2).)
- If
- PROVE that if the slopes of the sides of a triangle are
 (
( ), then the slopes of the medians do not form a geometric progression. (Use exercise 2 above.)
), then the slopes of the medians do not form a geometric progression. (Use exercise 2 above.) - Suppose that the slopes of the sides of a triangle form a geometric progression with common ratio
 , and that the slopes of the medians form a geometric progression with common ratio
, and that the slopes of the medians form a geometric progression with common ratio  . PROVE that:
. PROVE that:
 ;
; ;
; and
and  cannot have the same signs;
cannot have the same signs; and
and  cannot both be integers.
cannot both be integers.
- In
 , suppose that sides
, suppose that sides  have slopes
have slopes  , respectively. PROVE that:
, respectively. PROVE that:
- the median from vertex
 and the median from vertex
and the median from vertex  are perpendicular if and only if
are perpendicular if and only if  ,
,  ;
; - the median from vertex
 and the median from vertex
and the median from vertex  are perpendicular if and only if
are perpendicular if and only if  . Since this equation has no real solutions, does it imply that the median from vertex
. Since this equation has no real solutions, does it imply that the median from vertex  and the median from vertex
and the median from vertex  can never be perpendicular?
can never be perpendicular?
- the median from vertex
- Consider
 with vertices at
with vertices at  ,
,  , and
, and  . PROVE that:
. PROVE that:
- the slopes of the sides form a geometric progression in which
 ;
; - the median from vertex
 and the median from vertex
and the median from vertex  are perpendicular.
are perpendicular.
- the slopes of the sides form a geometric progression in which
- Find coordinates for the vertices of
 in which:
in which:
- the slopes of sides
 form a geometric progression with
form a geometric progression with  ;
; - the median from vertex
 and the median from vertex
and the median from vertex  are perpendicular.
are perpendicular.
- the slopes of sides
- Give an example of an isosceles triangle with slopes
 in which equation (1), namely
in which equation (1), namely  , is satisfied. (There are isosceles triangles (that are not equilateral) that satisfy equation (1).)
, is satisfied. (There are isosceles triangles (that are not equilateral) that satisfy equation (1).) - Let
 . PROVE that
. PROVE that  is a perfect square for
is a perfect square for  . Are these the only
. Are these the only  for which
for which  is a perfect square?
is a perfect square?